Page 1 of 1
Likninger med brøkuttrykk
Posted: 11/05-2018 13:18
by Andreashn
Hei er det noen som kan hjelpe meg med å forklare hvordan man løser oppgave 5.24 a,b,c i matematikk 1T
Det handler om likninger med brøkuttrykk og oppgavene er vedlagt som bilde
tusen takk for svar på forhånd
Andreas
Re: Likninger med brøkuttrykk
Posted: 11/05-2018 13:37
by Gjest10
Du må starta med å gange begge sider at likningen med felles nevnet. Deretter kan du løse oppgaven som en vanlig likning.
OBS!
Husk at svaret på likningen ikke kan gi 0 i nevner. Da er ikke det en løsning på likningen, eller så har ikke likningen en løsning.
Re: Likninger med brøkuttrykk
Posted: 11/05-2018 13:52
by Andreashn
Hei takk for svar.
Ja jeg har forsøkt det, men klarer ikke helt å finne fellesnevner etter likhetstegnet altså med 1. Blir da fellesnevneren 3*(x+3)(x-3) ?
Kan du hjelpe med et løsningsforslag her ?
tusen takk på forhånd,
Andreas
Re: Likninger med brøkuttrykk
Posted: 13/05-2018 00:44
by Myron
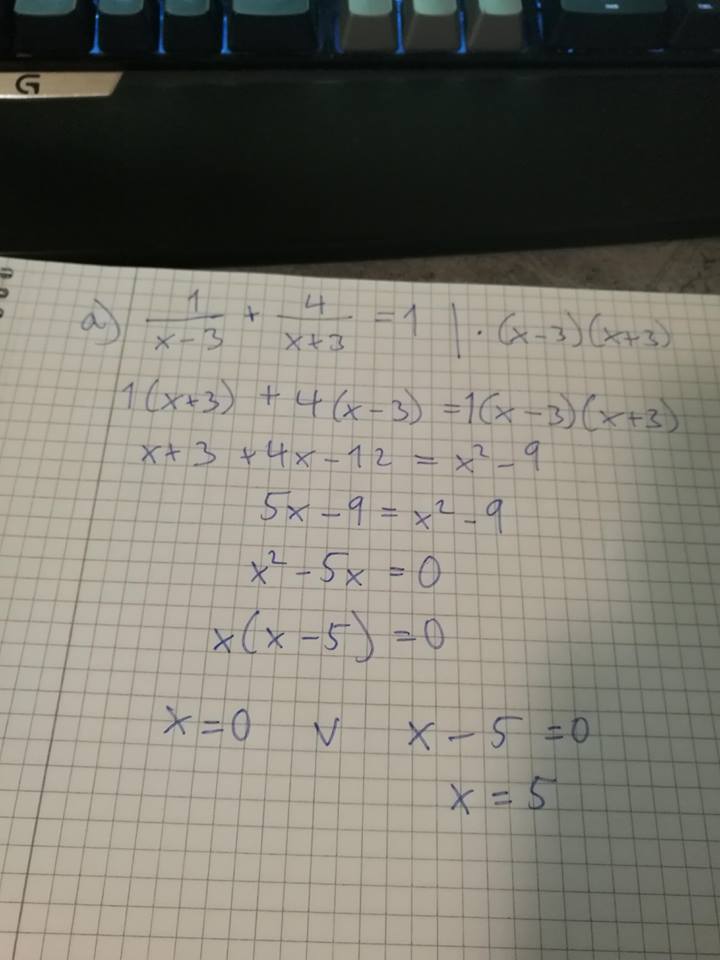
- Matt10.jpg (54.04 KiB) Viewed 2992 times
Her er mitt løsningsforslag til den første oppgaven. Spør hvis noe er uklart

Re: Likninger med brøkuttrykk
Posted: 13/05-2018 12:55
by Andreashn
Tusen hjertelig takk for svar og løsningsforslag. Tror jeg skjønte det meste nå takket være dette. tusen takk

et spørsmål på siste del, hvorfor blir x-5=0 og x=5 ? vet ikke om jeg skjønte helt dette
tusen takk
Re: Likninger med brøkuttrykk
Posted: 15/05-2018 01:55
by Gjest10
Vi har to uttrykk multiplisert med hverandre og gir 0. For at dette skal skje må x-verdien være slik at ett av uttrykkene blir lik 0 slik at 0*a=0. Her er uttrykken "x" og "x-5". Setter bare opp som to vanlige likninger og får 2 svar på likningen vi startet med.
Re: Likninger med brøkuttrykk
Posted: 16/05-2018 15:22
by Guest
Gjest10 wrote:Vi har to uttrykk multiplisert med hverandre og gir 0. For at dette skal skje må x-verdien være slik at ett av uttrykkene blir lik 0 slik at 0*a=0. Her er uttrykken "x" og "x-5". Setter bare opp som to vanlige likninger og får 2 svar på likningen vi startet med.
Tusen hjertelig takk for forklaringen. skjønte det nå

Andreas