v(t) = 12,42 - 0,0944t - 12,42*0,4937^t der t er tiden i sekunder fra start.
a) finn et uttrykk for akselrasjonen a(t). (her prøvde jeg å derivere siden a(t)=v'(t), men fikk ikke riktig svar.)
b) finn et uttrykk for forflytningen s(t). (her skal man vel antiderivere siden v(t)=s'(t).., men gjør noe feil her også)
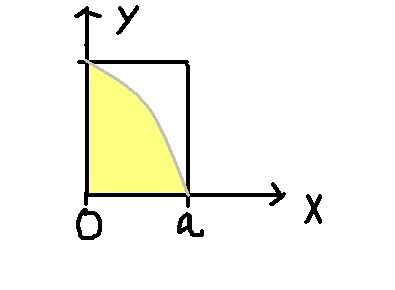
2) Figuren viser grafen til y = a^2 - x^2
vis at arealet av det gule området er 2/3 av rektangelets areal.