Eller ligningen til kurven etter ett kast?
Se bort i fra luftmotstand.
Jeg trenger en funksjon...
Moderators: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
Hva vet du fra før?
Cube - mathematical prethoughts | @MatematikkFakta
Med forbehold om tullete feil. (både her og ellers)
Med forbehold om tullete feil. (både her og ellers)
Et kast er en parabel.
Altså en funksjon på formen [tex]f(x)=ax^2+bx+c[/tex] der [tex]a < 0[/tex]
Eller mer avansert: http://en.wikipedia.org/wiki/Parabola
Altså en funksjon på formen [tex]f(x)=ax^2+bx+c[/tex] der [tex]a < 0[/tex]
Eller mer avansert: http://en.wikipedia.org/wiki/Parabola
http://projecteuler.net/ | fysmat
Jeg tenker som så, at uansett hvilken startfart du har på kastet, så vil gjenstanden følge en bestemt kurve. Og denne kurven kunne jeg tenke meg ett generelt utrykk for. Grunnlaget er for å finne en alternativ løsningsmetode for å regne ut toppunktet til kurven ved kast i oppover el nedoverbakke, der metoden jeg har er å dekomponere i X/Y- som følger bakken, ikke horisontalen
La fartsvektoren i det du kaster være [tex]\vec {v_0}[/tex]. Da vil posisjonen til legemet etter tiden t være [tex]\vec s(t) = \vec{v_0}t + \frac 12 \vec at^2[/tex], der [tex]\vec a = [0,\,-g][/tex].
Som du ser er dette også en parabel.
Som du ser er dette også en parabel.
-
Andreas345
- Grothendieck

- Posts: 828
- Joined: 13/10-2007 00:33
Er det denne du sikter til?
[tex]\vec r(t)=\left [v_{0}\cdot cos \alpha\cdot t, v_{0}\cdot sin \alpha\cdot t- \frac {1}{2}gt^2 \right ][/tex]
Dette er da vektorfunksjonen av et skrått kast, som vil beskrive bevegelsen i x og y retning.
Tegnforklaring:
[tex]\alpha[/tex]=er vinkelen startfarten danner med bakken.
[tex]v_0[/tex]= startfarten
[tex]g=9,81m/s^2[/tex]
[tex]\vec r(t)=\left [v_{0}\cdot cos \alpha\cdot t, v_{0}\cdot sin \alpha\cdot t- \frac {1}{2}gt^2 \right ][/tex]
Dette er da vektorfunksjonen av et skrått kast, som vil beskrive bevegelsen i x og y retning.
Tegnforklaring:
[tex]\alpha[/tex]=er vinkelen startfarten danner med bakken.
[tex]v_0[/tex]= startfarten
[tex]g=9,81m/s^2[/tex]
-
Vektormannen
- Euler

- Posts: 5889
- Joined: 26/09-2007 19:35
- Location: Trondheim
- Contact:
Har ikke dere skrevet samme greia på to forskjellige former da?
Elektronikk @ NTNU | nesizer
-
Andreas345
- Grothendieck

- Posts: 828
- Joined: 13/10-2007 00:33
Jo, men tok bare hensyn til dekomponering av fartsvektoren.
Hmmm...
Det dere sier, er at jeg bruker fartsloven og vinkelen...
Jeg skal bare forklare problemet og se om jeg tenker rett..
La oss si at du skyter ut en ball i bunnen av en bakke. Bakken heller 30°.
Ballen lander og blir liggede la oss si 50 meter oppe i bakken. Du skal finne høyeste punkt i forhold til bakken.
Ved horisontalt plan er det jo ikke noe probem, det er jo når Vy=0.
Men, når bakken skrår oppover/nedover, vil kurvens høyeste punkt være litt etter/før Vy=0
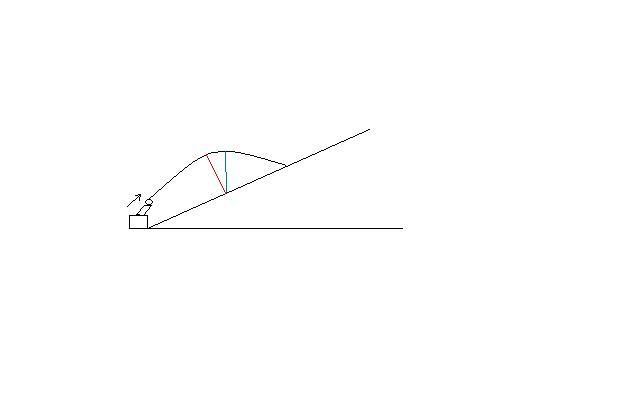
Rød strek, høyeste punkt i bakken.
Blå strek, høyeste i forhold til horisontalplanet, og der Vy= 0 (om jeg har forstått rett...!)
Det dere sier, er at jeg bruker fartsloven og vinkelen...
Jeg skal bare forklare problemet og se om jeg tenker rett..
La oss si at du skyter ut en ball i bunnen av en bakke. Bakken heller 30°.
Ballen lander og blir liggede la oss si 50 meter oppe i bakken. Du skal finne høyeste punkt i forhold til bakken.
Ved horisontalt plan er det jo ikke noe probem, det er jo når Vy=0.
Men, når bakken skrår oppover/nedover, vil kurvens høyeste punkt være litt etter/før Vy=0

Rød strek, høyeste punkt i bakken.
Blå strek, høyeste i forhold til horisontalplanet, og der Vy= 0 (om jeg har forstått rett...!)
Hvis du lar bakken ha helningen [tex]\alpha[/tex], så vil retningsvektoren til bakken være [tex]\vec b = [\cos\,\alpha,\,\sin\,\alpha][/tex]. Posisjonsvektoren til kastet er gitt ved [tex]\vec s(t) = \vec{v_0}t + \frac 12 \vec at^2[/tex], og farten ved [tex]\vec v(t) = \vec at + \vec{v_0}[/tex].
Er du enig i at den største høyden over bakken b er når [tex]\vec b\, ||\, \vec v(t)[/tex]?
(Jeg vet ikke om jeg er enig selv, bare tegnet litt kjapt på et ark. )
)
Er du enig i at den største høyden over bakken b er når [tex]\vec b\, ||\, \vec v(t)[/tex]?
(Jeg vet ikke om jeg er enig selv, bare tegnet litt kjapt på et ark.
Du kan jo ha noe der.. For når [tex][tex][/tex]\vec b\ er paralell med bakken, så er farten i Y-bakke- retning=0, ergo på sitt høyeste?Emomilol wrote:Hvis du lar bakken ha helningen [tex]\alpha[/tex], så vil retningsvektoren til bakken være [tex]\vec b = [\cos\,\alpha,\,\sin\,\alpha][/tex]. Posisjonsvektoren til kastet er gitt ved [tex]\vec s(t) = \vec{v_0}t + \frac 12 \vec at^2[/tex], og farten ved [tex]\vec v(t) = \vec at + \vec{v_0}[/tex].
Er du enig i at den største høyden over bakken b er når [tex]\vec b\, ||\, \vec v(t)[/tex]?
(Jeg vet ikke om jeg er enig selv, bare tegnet litt kjapt på et ark.)
Vel, i stedenfor [tex]\vec b\, ||\, \vec v(t)[/tex] som medfører [tex]k\cdot\vec b\, = \vec v(t)[/tex], kan du bytte om på komponentene i [tex]\vec b[/tex], og skifte fortegn på en av dem slik: [tex]\vec{b_{\perp}}=[-\sin\,\alpha,\,\cos\,\alpha][/tex]. Den nye vektoren står vinkelrett på [tex]\vec b[/tex], slik at du kan sette [tex]\vec{b_\perp} \cdot \vec v(t) = 0[/tex]. Her har du bare én variabel t, som burde gi deg (kun) én løsning [tex](t, \,\vec v(t))[/tex] . Den høyeste avstanden mellom [tex]\vec v(t)[/tex] og bakken, er da lengden av normalen fra dette punktet til bakken.

