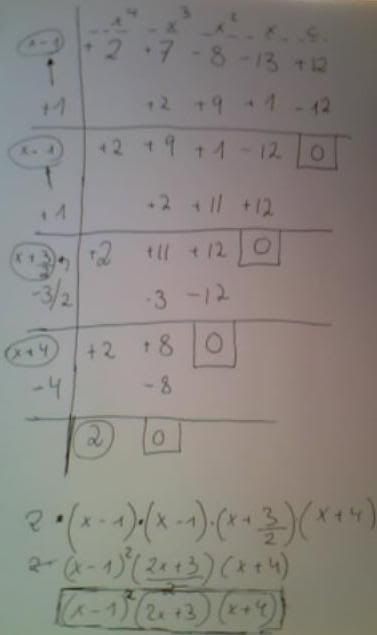
Jeg skal i denne artikkelen forklare hvordan å faktorisere et polynom [tex]P(x)[/tex] uten å kjenne til noen av røttene til dette polynomet(en rot til polynom [tex]P(x)[/tex] er det nummeret som vis du bytter ut med [tex]x[/tex] gir [tex]P(x)=0[/tex]).
Først må vi ha kjensel til 2 ting:
1.- Ruffini's regel
2.- The rational root theorem
1.-Ruffini's regel
Ruffini's regel kan bare brukes til å dele et polynom [tex]P(x)[/tex] på [tex]r[/tex], hvis [tex]r=x-a[/tex] eller [tex]r=x+a[/tex], altså kan [tex]r[/tex] bare være et første grads polynom.
Hvis du har [tex]P(x)=x^2+4x-21[/tex] og vil dele det på [tex]r=x-3[/tex] så:
1.- I [tex]P(x)[/tex] fjerner bokstav delen i polynomet [tex]x[/tex]ene([tex]x, x^2, x^3.....[/tex]), slik at du får [tex]1 + 4 -21[/tex]
og
2.- I [tex]r[/tex], så fjerner man [tex]x[/tex] og bytter på fortegnet til a(altså nummeret som står etter [tex]x[/tex]), slik at du får [tex]+ 3[/tex]
Vi innfører da:
.....|1 + 4 - 21
+3 |_ + 3 + 21
.....|1 + 7 + 0
Beskriving:
du tar altså det nummeret som er mest til venstre i [tex]P(x)[/tex](altså 1 her) og direkte putter det under streken. Vi ganger da [tex]r[/tex](husk hva vi gjorde i punkt 2) med dette nummeret vi puttet under streken(1) og resultatet(+3) skriver vi under tallet som er til venstre til forrige tall i [tex]P(x)[/tex](altså under +4). Vi summer da disse to nummeren(+3+4) og resultatet(+7) setter vi under streken. Vi ganger dette resultatet(+7) med [tex]r[/tex](altså [tex]3\cdot7[/tex]). Vi putter resultatet(+21) under tallet som er til venstre til forrige tall(-21) i [tex]P(x)[/tex] og summer på nytt igjen(-21+21), og for 0. Hvis polynomet hadde vært av høyere grad så ville dette gått videre.(Forklarer hav jeg mener med dette i morra)
vi for altså som resultat 1 + 7 + 0, hvor da vi trekker fra 0 så blir det 1+7. Da setter vi opp x ved siden av nummerne, ved å begynne fra høre side til venstre. Første nummer fra venstre får [tex]x^0[/tex], neste får [tex]x^1[/tex], neste får [tex]x^2[/tex] også videre.. altså i dette eksemplet så for vi [tex]7x^0+1x^1[/tex](husk vi begyner fra venstre side) som altså er lik [tex]7\cdot1+1x=x + 7[/tex] Som dere kanskje har funnet ut er dette nummeret den andre faktoren([tex]x-3[/tex] var den ene husker dere?)
Eksempel med bilder:
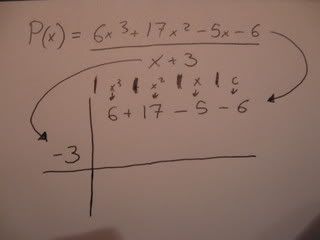
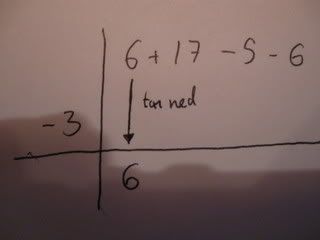
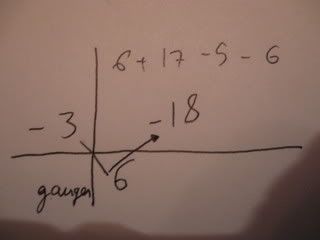
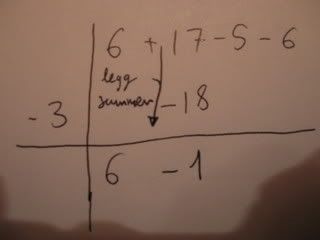
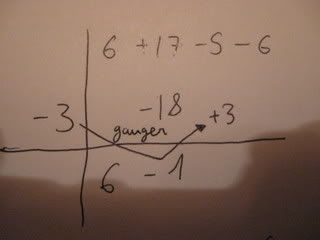

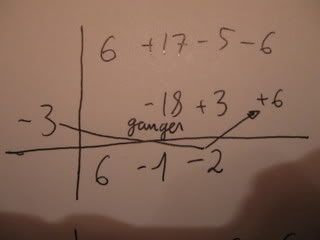
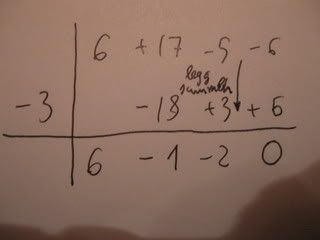
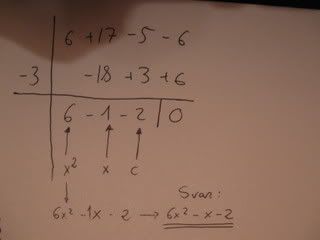
Den metoden kan altså brukes for [tex]P(x)[/tex] i hvilken grad, men som sagt husk [tex]r=x\pm{a}[/tex]
Skjekke denne siden for mere spesifik forklaring(*engelsk side)
Ganske enkelt ikke sant?
2.- Rational root theorem
Denne regelen sier at i et polynom
[tex]P(x)=a+bx^1+cx^2......dx^{n-1}+ex^n[/tex]
så er en av røtten til [tex]P(x)[/tex] er [tex]\frac{p}q[/tex] der hvor p er altså en faktor av a og q en faktor av [tex]e[/tex](der hvor [tex]e[/tex] er tallet i polynomet med høyeste grad i [tex]P(x)[/tex] og [tex]a[/tex] konstanten i [tex]P(x)[/tex] ; se eksempel)
Aplikasjon
Vis vi i ruffini ikke kjenner til [tex]r[/tex], så må vi prøve og feile, for å finne ut hvilket tall(i [tex]r[/tex]) får [tex]P(x)[/tex] til å bli 0. Vi vet at [tex]P(x)=0[/tex] Når:
Dette skjer
.....|1 + 4 - 21
+3 |_ + 3 + 21
.....|1 + 7 + 0
Dere ser nulleren ikke sant?
Så vi må altså finne et tall som får det siste tallet i summen i ruffinis metode til å bli 0. Vi kan altså som sagt prøve å feile med all nummeren vi vil, men det kan ta oss timer, vis for å ikke si dager. Derfor bruker vi the ratioanl root theorem til å si oss at:
Det tallet som er på venstre side når vi bruker ruffini's metode er = [tex]\frac{\pm{p}}\pm{q}[/tex] der hvor [tex]q=[/tex] en av faktorene til 1. tallet(i øverste linje) som er på høyre side i ruffnis metode og [tex]p=[/tex] er en faktor i siste tallet(i øverste linje)på høyre side. Husk at p og q kan være positiv og negativ.
Vi ser altså at i eksemplet så er +3 en faktor av 21. Vi vet også at i eksemplet så er -7 rot av [tex]P(x)x + 4 - 21[/tex], så kan vi da bruke -7 i stedet for +3 for å dele? så klart det er jo en rot av [tex]P(x)[/tex]. Som vi ser, så er jo 7 en faktor av 21, bare i negativ form. Vis vi ikke hadde kjent til røtten til [tex]P(x)[/tex], så kunne vi ha kommet fram til at en rot er [tex]\frac{p}q[/tex], altså [tex]\pm[/tex]en faktor av 21 delt på [tex]\pm[/tex] en faktor av 1. da har vi 6 muligheter, -3, +3, -7, +7 og -21, +21. Vi prøver da og finner ut at vi får 0 med +3(som fører til faktoren [tex]x+7[/tex]) og -7( som fører til faktoren [tex]x+3[/tex]).
Vi omdanner da tengenen på disse tallene, og legger til x. Faktorene er dermed [tex]x+7[/tex] og [tex]x+3[/tex], altså så er [tex]P(x)=x^2+4x-21=(x+7)(x-3)[/tex]
Et tips kan også være å prøve seg fram med et tall, og vis du ser at tallene i ruffinis metode blir bare større og større, så ikke set in noe tall større en forrige
Jeg har satt opp et ganske basisk polynom her. Der kan bruke denne metoden tile polynomer som har opp til grad 5. Det er eksempler litt lengre forran på mere kompliserte polynomer.
Bruk samme metode på andre polynomer og prøv dere frem.
Tar gjerne i mot tilbakemeldinger og spørsmål, og eventuelt informasjon om feiler som denne teksten kan inneholde
MVH
Thales