En ellipse med halvakser a og b og sentrum i origo har likningen;
[tex]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/tex]
e) Finn volumet av den figuren vi får når vi dreier ellipsen 180 grader om x-aksen.
Man får jo halvsirkel når man dreier ellipsen 180 graderom x-aksen.Blir det da riktig å sette for å finne volumet;
[tex]V=\pi \int_{a}^{b} (\frac{x^2}{a^2}+\frac{y^2}{b^2})^2 dx[/tex] ?
På forhånd takk!
Ellipse
Moderators: Aleks855, Gustav, Nebuchadnezzar, Janhaa, DennisChristensen, Emilga
Vet ikke helt om du kan kalle det en halvsirkel, men jo, det stemmer at vi får et omdreiningslegeme som formelen din ser mer eller mindre riktig ut for. Problemet ditt er dog at uttrykket du setter inn ikke er en funksjon av èn variabel. Mulig noen som har mer peiling enn meg kan fortelle hvordan dette er fullt lovlig så lenge du har svart belte i Kalkulus, men skal vi holde oss til måten du ser ut til å planlegge å løse dette på må du først skrive likningen din om til en funksjon av bare èn variabel.
Ser du på figuren likningen din skisserer, som er en ellipse, ser du fort at dette kan være umulig. Til én verdi av x vil det være to funksjonsverdier og så videre. Det du burde gjøre er å finne ett funksjonsuttrykk for den delen av ellipsen som ligger over x-aksen. Dette er fullt mulig. Så kan du plugge det rett inn i formelen din for volumet av et omdreiningslegeme.
EDIT: Og før jeg glemmer det ser du også ut til å ha klusset bittelitt med grensene i integralet ditt. Prøv å tegne opp ellipsen som oppstår av likningen din og se hvor grensene burde gå.
Ser du på figuren likningen din skisserer, som er en ellipse, ser du fort at dette kan være umulig. Til én verdi av x vil det være to funksjonsverdier og så videre. Det du burde gjøre er å finne ett funksjonsuttrykk for den delen av ellipsen som ligger over x-aksen. Dette er fullt mulig. Så kan du plugge det rett inn i formelen din for volumet av et omdreiningslegeme.
EDIT: Og før jeg glemmer det ser du også ut til å ha klusset bittelitt med grensene i integralet ditt. Prøv å tegne opp ellipsen som oppstår av likningen din og se hvor grensene burde gå.
Prøv å be MatteNoob om unnskyldning du, så tror jeg han kan hjelpe deg.
Det er ikke alltid slik at humor er så enkelt å forstå. Særlig når den formidles skriftlig, som her inne...
Svaret som du fikk her av Karl_Erik er selvsagt helt fint det!
Det er ikke alltid slik at humor er så enkelt å forstå. Særlig når den formidles skriftlig, som her inne...
Svaret som du fikk her av Karl_Erik er selvsagt helt fint det!
Først finner jeg altså funksjonsuttrykk for gjenstanden som er over x-aksen.
Funksjonsuttrykket:
[tex]f(x)=x^2[/tex] for gjenstanden eller er denne kun for den ene halvaksen? Hvis det er for den ene så blir vel ved å ta med den andre [tex]2x^2[/tex] Eller er jeg bare helt ut og kjører meg vilt?
EDIT:Det har vært en lang saklig og hyggelig prosess for unnskyldningen til Mattenooben.
Funksjonsuttrykket:
[tex]f(x)=x^2[/tex] for gjenstanden eller er denne kun for den ene halvaksen? Hvis det er for den ene så blir vel ved å ta med den andre [tex]2x^2[/tex] Eller er jeg bare helt ut og kjører meg vilt?
EDIT:Det har vært en lang saklig og hyggelig prosess for unnskyldningen til Mattenooben.
Volumet av et omdreiningslegeme er gitt ved formelen:
[tex]V = \int_{x_1}^{x_2} (f(x))^2 dx[/tex]
Der [tex]f(x)[/tex] er den funskjonen som rorterer rundt [tex]x[/tex]-aksen, og [tex]x_1[/tex] og [tex]x_2[/tex] er der omdreiningslegeme "starter" og "slutter".
Hva er så [tex]f(x)[/tex] ?
Tips:
Prøv å snu på likningen [tex]\frac{x^2}{a^2} + \frac{y^2}{b^1}= 1[/tex]
slik at du har [tex]y = ....[/tex] , dvs y alene på venstre side. (Eller evt. [tex]y^2[/tex])
Hvorfor tror du jeg tipser deg slik?
[tex]V = \int_{x_1}^{x_2} (f(x))^2 dx[/tex]
Der [tex]f(x)[/tex] er den funskjonen som rorterer rundt [tex]x[/tex]-aksen, og [tex]x_1[/tex] og [tex]x_2[/tex] er der omdreiningslegeme "starter" og "slutter".
Hva er så [tex]f(x)[/tex] ?
Tips:
Prøv å snu på likningen [tex]\frac{x^2}{a^2} + \frac{y^2}{b^1}= 1[/tex]
slik at du har [tex]y = ....[/tex] , dvs y alene på venstre side. (Eller evt. [tex]y^2[/tex])
Hvorfor tror du jeg tipser deg slik?
Det kan være lærerikt å lese litt om ellipser på wikipedia. Dessuten er denne interaktive java appleten fin å bruke for å forstå egenskapene og uttrykket for en ellipse.
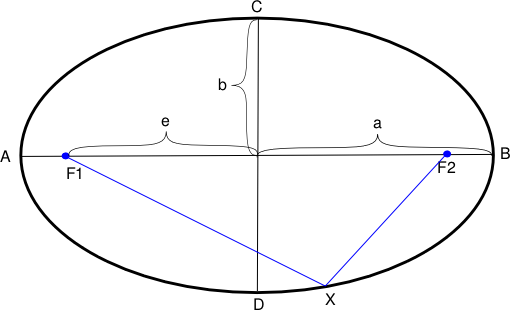
Vi vil uttrykke ellipsen ved x. Dessuten er a & b konstanter.
[tex]\frac {x^2}{a^2}+ \frac {y^2}{b^2} = 1 \\ \, \\ y^2 = \left(1-\frac{x^2}{a^2}\right)\cdot b^2 \\ \, \\ y = \sqrt{\left(1-\frac{x^2}{a^2}\right)\cdot b^2} \\ \, \\ y = \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex]
Videre har vi at [tex]180\textdegree = \pi \, \rm{rad}[/tex]
Jeg kan ikke love at alt jeg har gjort her er riktig, for ellipser kan jeg ikke så mye om, men dette er nok greit. Dog finner jeg ikke grensene for integralet i teksten din, mulig disse er utelatt, eller at de er a, b ? Ikkje veit eg.
EDIT:
Ved ettertanke husker jeg at dersom man skal dreie et legeme 360 grader om x-aksen, har vi
[tex]\pi \cdot \int_a^b (f(x))^2 \rm{d}x[/tex]
Så da antar jeg at vi dreier 180 grader om x-aksen dersom vi setter
[tex]\frac \pi 2 \cdot \int_a^b (f(x))^2 \rm{d}x[/tex]

Vi vil uttrykke ellipsen ved x. Dessuten er a & b konstanter.
[tex]\frac {x^2}{a^2}+ \frac {y^2}{b^2} = 1 \\ \, \\ y^2 = \left(1-\frac{x^2}{a^2}\right)\cdot b^2 \\ \, \\ y = \sqrt{\left(1-\frac{x^2}{a^2}\right)\cdot b^2} \\ \, \\ y = \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex]
Videre har vi at [tex]180\textdegree = \pi \, \rm{rad}[/tex]
Nei, man får ikke en halvsirkel, men volumet av ei "bolle" når man dreier den 180 grader om x-aksen. Dessuten er det viktig å merke seg at dersom a=b, så får vi en halvsirkel ved å nytte det overnevnte funksjonsuttrykket. Da a=b=r, radius i en sirkel.Wentworth wrote:En ellipse med halvakser a og b og sentrum i origo har likningen;
[tex]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/tex]
e) Finn volumet av den figuren vi får når vi dreier ellipsen 180 grader om x-aksen.
Man får jo halvsirkel når man dreier ellipsen 180 graderom x-aksen.Blir det da riktig å sette for å finne volumet;
[tex]V=\pi \int_{a}^{b} (\frac{x^2}{a^2}+\frac{y^2}{b^2})^2 dx[/tex] ?
På forhånd takk!
Jeg kan ikke love at alt jeg har gjort her er riktig, for ellipser kan jeg ikke så mye om, men dette er nok greit. Dog finner jeg ikke grensene for integralet i teksten din, mulig disse er utelatt, eller at de er a, b ? Ikkje veit eg.
EDIT:
Ved ettertanke husker jeg at dersom man skal dreie et legeme 360 grader om x-aksen, har vi
[tex]\pi \cdot \int_a^b (f(x))^2 \rm{d}x[/tex]
Så da antar jeg at vi dreier 180 grader om x-aksen dersom vi setter
[tex]\frac \pi 2 \cdot \int_a^b (f(x))^2 \rm{d}x[/tex]
Øver du til eksamen i matematikk? Se eksamensoppgaver med løsningsforslag.
Vil du ha egen webside, se her for å lage hjemmeside.
Vil du ha egen webside, se her for å lage hjemmeside.
[tex]\pi \cdot \int_a^b {(\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}})}^2 dx[/tex]
[tex]\frac {\pi} {2} \cdot \int_a^b {(\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}})}^2 dx[/tex]
Jeg har prøvd meg litt fram og begge disse to integralene ga meg ikke riktig svar.
b er øvre og a er nedre integrasjonsgrense. Det riktige svaret skal være : [tex]\frac{4}{3} \pi ab^2[/tex]
EDIT:Ettam: Tipser slik for at jeg skulle kunne finne den riktige funksjonen...
[tex]\frac {\pi} {2} \cdot \int_a^b {(\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}})}^2 dx[/tex]
Jeg har prøvd meg litt fram og begge disse to integralene ga meg ikke riktig svar.
b er øvre og a er nedre integrasjonsgrense. Det riktige svaret skal være : [tex]\frac{4}{3} \pi ab^2[/tex]
EDIT:Ettam: Tipser slik for at jeg skulle kunne finne den riktige funksjonen...
Her burde du fått:MatteNoob wrote: Vi vil uttrykke ellipsen ved x. Dessuten er a & b konstanter.
[tex]\frac {x^2}{a^2}+ \frac {y^2}{b^2} = 1 \\ \, \\ y^2 = \left(1-\frac{x^2}{a^2}\right)\cdot b^2 \\ \, \\ y = \sqrt{\left(1-\frac{x^2}{a^2}\right)\cdot b^2} \\ \, \\ y = \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex]
[tex]y = \pm \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex]
Der [tex]y = +\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex] er den øverste halvdelen av ellipsen. Mens [tex]y = -\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex] er den nederste halvden (den under [tex]x[/tex]-aksen).
Bruker denne: [tex]y = +\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex], og roterer den [tex]360 \textdegree[/tex] rundt x-aksen:
[tex]V = \pi \int_{-a}^a \left( \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}} \right)^2 dx = \pi \int_{-a}^a \left(b^2 - \frac{x^2 \cdot b^2}{a^2} \right) dx = \pi \left[b^2 x - \frac{x^3 \cdot b^2}{3a^2} \right]_{-a}^a \, = \pi\left(b^2a - \frac{a^3 \cdot b^2}{3a^2} - \left( - b^2a + \frac{a^3 \cdot b^2}{3a^2}\right)\right) = \pi\left(2b^2a - \frac{2a \cdot b^2}{3}\right) = \frac{4}{3}\pi ab^2[/tex]
[tex]V = \pi \int_{-a}^a \left( \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}} \right)^2 dx = \pi \int_{-a}^a \left(b^2 - \frac{x^2 \cdot b^2}{a^2} \right) dx = \pi \left[b^2 x - \frac{x^3 \cdot b^2}{3a^2} \right]_{-a}^a \, = \pi\left(b^2a - \frac{a^3 \cdot b^2}{3a^2} - \left( - b^2a + \frac{a^3 \cdot b^2}{3a^2}\right)\right) = \pi\left(2b^2a - \frac{2a \cdot b^2}{3}\right) = \frac{4}{3}\pi ab^2[/tex]
Ja, det har du helt rett i, takk for rettelsen. Den første var en "glemmefeil", men det slo meg ikke, så da er det samme hvordan feil det er, for det er fortsatt feil, hehe. Løsningen din var opplysende for meg, men kunne du ikke ha satt [tex]\color{red}2[/tex][tex]\pi \int_0^a\left(f(x)\right)^2 \rm{d}x[/tex] for å forenkle valideringen av grensene litt? Denne figuren er jo symmetrisk (med y-aksen som symmetrilinje)ettam wrote:Her burde du fått:
[tex]y = \pm \sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex]
Der [tex]y = +\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex] er den øverste halvdelen av ellipsen. Mens [tex]y = -\sqrt{b^2 - \frac{x^2 \cdot b^2}{a^2}}[/tex] er den nederste halvden (den under [tex]x[/tex]-aksen).
Helt sikkert fordi du vil at han skal tenke selv og forstå sammenhengen mellom algebra og figuren? Hehe, jeg gir ham en oppgave der han må gjøre litt... Så:Ettam wrote:Hvorfor tror du jeg tipser deg slik? (til Wentworth)
@ Wentworth:
Denne oppgaven er til deg:
Bevis at formelen for volumet av ei kule er [tex]\text{V} = \frac 43\pi r^3[/tex]
Når du får opplyst at:
[tex](x-x_0)^2 + (y-y_0)^2 - r^2 = 0[/tex]
Denne burde absolutt være overkommelig for deg dersom du forsto hva som virkelig "skjedde" under løsningen av denne oppgaven! :]
Øver du til eksamen i matematikk? Se eksamensoppgaver med løsningsforslag.
Vil du ha egen webside, se her for å lage hjemmeside.
Vil du ha egen webside, se her for å lage hjemmeside.
MatteNoob wrote: @ Wentworth:
Denne oppgaven er til deg:
Bevis at formelen for volumet av ei kule er [tex]\text{V} = \frac 43\pi r^3[/tex]
Når du får opplyst at:
[tex](x-x_0)^2 + (y-y_0)^2 - r^2 = 0[/tex]
Denne burde absolutt være overkommelig for deg dersom du forsto hva som virkelig "skjedde" under løsningen av denne oppgaven! :]
Fin oppgave, MatteNoob. En liten forglemmelse i teksten bare, derfor legger jeg den ut på nytt:
- @ Wentworth:
Denne oppgaven er til deg:
Bevis at formelen for volumet av ei kule er [tex]\text{V} = \frac 43\pi r^3[/tex]
Når du får opplyst at en sirkel med sentrum i [tex](x_0, y_0)[/tex] og radius [tex]r[/tex] har likningen:
[tex](x-x_0)^2 + (y-y_0)^2 - r^2 = 0[/tex]
Denne burde absolutt være overkommelig for deg dersom du forsto hva som virkelig "skjedde" under løsningen av denne oppgaven! :]
Sikkert innlysende det jeg la til, men det bør være med.
Jo, det stemmer det.MatteNoob wrote:men kunne du ikke ha satt [tex]\color{red}2[/tex][tex]\pi \int_0^a\left(f(x)\right)^2 \rm{d}x[/tex] for å forenkle valideringen av grensene litt? Denne figuren er jo symmetrisk (med y-aksen som symmetrilinje)
Denne oppgaven likte jeg ,her beviser jeg [tex]V=\frac{4}{3} \pi r^3[/tex];
Jeg tenker slik: Tegner ei kule for deretter å sette en kordinatakse x med origo 0 i sentrum av kulen, da vet jeg at denne kulen strekker seg fra [tex]x=-r[/tex] til [tex]x=r[/tex].
Deretter setter jeg inn en snittflate som er en sirkel med radius (y(x))^2, denne radiusen er altså da lik ifølge oppgaven når jeg har løst likningen [tex]r^2 - x^2[/tex]
Videre vet jeg at da er arealet [tex]A(x)=\pi ( y(x))^2=\pi (r^2-x^2)[/tex] Og det gir dette volumet;
[tex]V=\int_{-r}^{r} A(x) dx=\pi \int_{-r}^{r} (r^2-x^2)dx=\pi[r^2x - \frac{1}{3}x^3]_{-r}^{r}=\pi((r^3- \frac{1}{3}r^3)-(-r^3-\frac{1}{3}(-r^3)))=\pi(\frac{2}{3}r^3 + \frac{2}{3}r^3)=\frac{4}{3}\pi r^3[/tex]
Jeg tenker slik: Tegner ei kule for deretter å sette en kordinatakse x med origo 0 i sentrum av kulen, da vet jeg at denne kulen strekker seg fra [tex]x=-r[/tex] til [tex]x=r[/tex].
Deretter setter jeg inn en snittflate som er en sirkel med radius (y(x))^2, denne radiusen er altså da lik ifølge oppgaven når jeg har løst likningen [tex]r^2 - x^2[/tex]
Videre vet jeg at da er arealet [tex]A(x)=\pi ( y(x))^2=\pi (r^2-x^2)[/tex] Og det gir dette volumet;
[tex]V=\int_{-r}^{r} A(x) dx=\pi \int_{-r}^{r} (r^2-x^2)dx=\pi[r^2x - \frac{1}{3}x^3]_{-r}^{r}=\pi((r^3- \frac{1}{3}r^3)-(-r^3-\frac{1}{3}(-r^3)))=\pi(\frac{2}{3}r^3 + \frac{2}{3}r^3)=\frac{4}{3}\pi r^3[/tex]


