Din løsning gir: [tex]15,15499889[/tex]
Den egentelige løsningen gir: [tex]15,15367058[/tex]
[tex]1,328313767 \cdot 10^{-3}[/tex] forskjell.
Moderatorer: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
Jeg sa at det var en feilKarl_Erik skrev:Mulig jeg misforstår her, men går du ikke utifra at utgangsvinkelen med bakken er den samme som vinkelen mellom det høyeste punktet, startpunktet og bakken er det samme når den faktisk er en del mindre? Eller har jeg lest innlegget ditt feil?
Kan faktisk bevise det nåmathme skrev:Hvordan kom du fram til det ?Thales skrev:Forresten, jeg fant ut at:
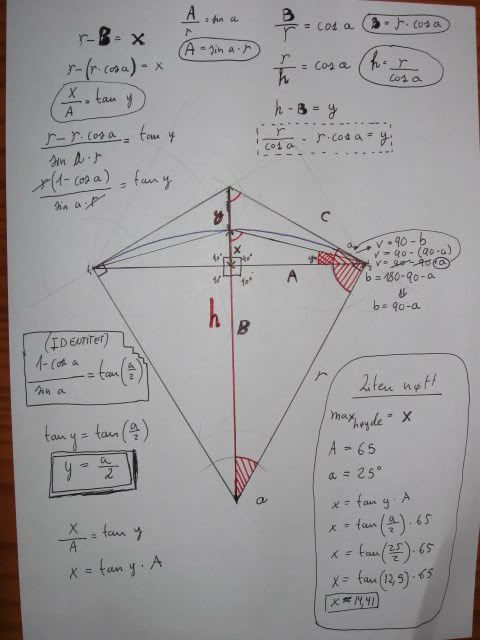
[tex]max_{hoeyde}=\frac{tan(25)\cdot\frac{130}{2}}{2}=\frac{tan(25)\cdot{65}}{2}[/tex]
Noen som klarer å forklare hvorfor?
Nehei ? Hadde vært utrolig kult!Thales skrev:Kan faktisk bevise det nåmathme skrev:Hvordan kom du fram til det ?Thales skrev:Forresten, jeg fant ut at:
[tex]max_{hoeyde}=\frac{tan(25)\cdot\frac{130}{2}}{2}=\frac{tan(25)\cdot{65}}{2}[/tex]
Noen som klarer å forklare hvorfor?

I dette tilfellet er parabelen er en del av en sirkel ikke sant?Bogfjellmo skrev:Mulig jeg misforstår noe her, Thales, men antar du i beviset at ballen følger en sirkelbane? Det er nemlig ikke korrekt, den følger en parabel.
Vi legger kastet inn i et koordinatsystem; y-aksen loddrett oppover og x-aksen bortover langs horisontalplanet. En vektorfunksjon som gir posisjonsvektoren til ballen erJarle10 skrev:Oppfølger:
Hvis baseballspilleren skyter ballen med en vinkel [tex]\theta[/tex] på den skrå bakken som har vinkelen [tex]\phi[/tex] med horisontalplanet, hvor stor må starthastigheten være om han ønsker å skyte den bort med lengden [tex]L[/tex] langs skråplanet?
Vinklene er slik at summen av dem er mindre enn 90 grader.
Hva er maksimalhøyden på ballen?