Noen som kan hjelpe litt med fremgangsmåte på denne?
Har prøvd begge desse metodene, men får så stygge uttrykk

Prøvde på denne selv, stemmer (3/4)*Pi?

Gledeleg å høyre at du har kome i mål. Vil gjerne legge til at vi kan sjekke sluttresultatet ved ein relativt enkel figuranalyse:

Romfiguren er ein sylinder med radius r = 5 og høgde h = 7. Den sirkelforma grunnflata ligg i xy-planet og har sentrum i origo.
Sylinderaksen går langs z-aksen , dvs ...

\overrightarrow{k} er einingsvektor langs z-aksen. Dette er ein konstant som vi kan setje utanfor integralteiknet.

NÅr vi har integrert opp r-delen og z-delen , endar vi opp med eit reelt tal multiplisert med \overrightarrow{k} ( \overrightarrow{i} -delen og \overrightarrow{j} -delen blir begge ...

Først må vi finne massen M til romfiguren:

M = \int \int \int \rho (x,y,z) dV = ( innfører sylinderkoordinatar ) 6 \int_{0}^{2\pi } ( \int_{0}^{7} ( \int_{0}^{5} ( r + z ) r dr) dz) d \varphi

Massesenteret ( \overline{x} , \overline{y} , \overline{z} ) =

\int \int \int ( \overrightarrow{r ...

Hvordan løser man en slik oppgave? Finner ingen lignende eksempel i boka eller på nett, og jeg har ramlet helt av dobbel/trippel-integraltoget...

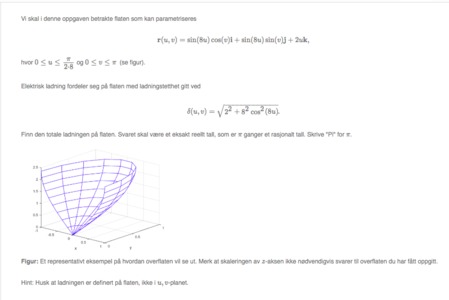
Hei, har nesten akkurat samme oppgave, bare ulike tall. Har funnet mine integrasjonsgrense (0<r<36 og 0<@<pi/2), men skjønner ikke noe veldig viktig, nemlig hvordan uttrykket jeg skal integrere ser ut! Har jo gjort om til polarkoordinater for å finne r, men ja, hva skal jeg integrere? Dere kan ta ...

Skriv lagrange-multiplikatoren-funksjonen som \mathcal{L}(x,y,\lambda)=f(x,y)+\lambda g(x,y) og sett gradienten av systemet lik null.

Da vil du få et likningssystem med tre likninger hvor den tredje likningen er grenseområdet ditt, dvs. kurven x^4+y^2=4 .

Altså

\begin{cases} 4x-4x^3+4\lambda x ...

Vi kommer aldri helt overens. Jeg trenger hjelp til oppg. b. Har gjort så langt jeg klarer, men er usikker på hvordan jeg ror i land det siste