Forskjell mellom versjoner av «1T 2012 januar LØSNING»
(→a)) |
|||
| Linje 126: | Linje 126: | ||
===a)=== | ===a)=== | ||
| − | Sylinder der d + h = 6, d = 2r, og $V = \ | + | Sylinder der d + h = 6, d = 2r, og $V = \pi r^2h$. Vi får: |
| − | |||
| − | |||
| − | |||
===b)=== | ===b)=== | ||
Revisjonen fra 27. des. 2013 kl. 08:00
Løsningsforslag laget av Nebu (pdf)
DEL EN
Oppgave 1:
a)
$\frac{x^2-25}{x^2+10x+25} = \frac{(x+5)(x-5)}{(x+5)(x+5)} = \frac{x-5}{x+5}$
b)
$3^{2x-1} = 1 \\ 3^{2x-1} = 3^0 \\ 2x-1 =0 \\ x = \frac 12$
c)
$\frac{a^{\frac 14}\cdot \sqrt a}{(a^{\frac 34})^3 \cdot a^{-2}} = \frac{a^{\frac14} \cdot a^{\frac 12}}{a^{\frac94} \cdot a^{-2}} = a^{\frac14 + \frac 24 - \frac 94 + \frac 84} = a ^{\frac 12} = \sqrt a$
d)
Areal av trekant er: $A = \frac{3 \cdot 4}{2} =6$
Høyden på Figur er h: $A = \frac{gh}{2} \Rightarrow h=\frac{2A}{g} = \frac{2 \cdot 6}{5} = 2,4$
e)
1) $\quad f(x) \leq 0 \quad x \in < \leftarrow, 1] \cup [ 3, \rightarrow>$
2) $\quad fx) > g(x) \quad x \in < \leftarrow, 0 > \cup <5, \rightarrow >$
f)
$ \tan c =\frac{motstående katet}{hosliggende katet} \Rightarrow 2= \frac{3}{AC} \Rightarrow AC = \frac 32$
g)
1) $\quad P(ikke-grønn) = \frac {5}{6} \cdot \frac {4}{5} = \frac 23$
2) $P(en-blå-og-en-rød) = \frac{3}{6} \cdot \frac{2}{5} + \frac{2}{6} \cdot \frac{3}{5} = \frac{12}{30} = \frac 25$
h)
$f(x)=x^2 + 1 \\ f´(x) = lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \\=lim_{\Delta x \rightarrow 0} \frac{(x+ \Delta x)^2+1 - (x^2+1) }{\Delta x} \\ =lim_{\Delta x \rightarrow 0} \frac{x^2+2 x\Delta x + (\Delta x)^2+1 - x^2-1 }{\Delta x} \\ = lim_{\Delta x \rightarrow 0} \frac{2 x\Delta x + (\Delta x)^2 }{\Delta x} \\ =lim_{\Delta x \rightarrow 0} 2 x + \Delta x \\ = 2x$
Oppgave 2
a)
$f(x)= -x^2+2x-2 \\ b^2-4ac = 4 - 4 \cdot 2 = -4$
Siden tallet under rottegnet i abc formelen er negativt har likningen f(x) = 0 ingen løsning og f(x) har ingen nullpunkter.
b)
$f´(x) = -2x+2 \\ f´(x) = 0 \\ -2x+2=0 \\ x= 1 \\f(1) = -1$
Funksjonen har et maksimumspunkt i (1,-1). (Andregradsfunksjoner med negativ faktor forran andregradsleddet har alltid et maksimum).
(dette er del en så du må lage en verditabell og tegne grafen for hånd)
c)
$f´(2) =-2 \\ y =ax + b \\ -2 = -2 \cdot 2 + b \\ b=2 \\ y= -2x + 2$
Finnen først stigningstallet i punktet, ved hjelp av den deriverte. Setter så stigningstallet og verdiene for x og y inn i likningen for den rette linje, for å finne b. Likningen til tangenten i punktet (2, -2) er altså y = -2x + 2.
Oppgave 3
a)
Tilnærmet : F = 2C +30
Nøyaktig: 5F = 9C + 160
$100^{\circ}$ C til Fahrenheit:
Tilnærmet: F= 230
Nøyaktig: 5F = 900 +160, dvs. F= 212
Forskjellen er på 18 Fahrenheit, der den tilnærmede modellen gir for høy verdi.
b)
F= 2C + 30
5F = 9C + 160
10C + 150 = 9C + 160
C=10 og F=50
Den forenklede modellen er mest nøyaktig i området rundt 10 grader Celsius eller 50 Fahrenheit. Akkurat på 40/50 er den forenklede modellen helt nøyaktig.
DEL TO
Oppgave 4
a)
Dersom trekanten er rettvinklet må Pytagoras gjelde og den lengste siden må være hypotenus.
$(6,0 cm)^2 = 36,0 cm^2 \\ (4,0 cm)^2 + (5,0 cm)^2 = 16,0cm^2+25,0cm^2= 41,0cm^2$
Hvilket viser at trekanten ikke er rettvinklet.
b)
Når man kjenner alle sidene i en trekant bruker man cosinussettningen til å finne en vinkel, deretter kan man bryke arealsettningen til å finne arealet av trekanten.
$a^2=b^2+c^2-2ab\cos C \Rightarrow \cos C = \frac{a^2-b^2-c^2}{-2ab}$
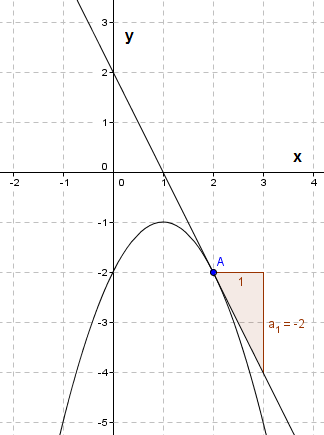
c)
Oppgave 5
a)
Sylinder der d + h = 6, d = 2r, og $V = \pi r^2h$. Vi får: