1P 2025 vår LK20 LØSNING

DEL EN

Oppgave 1

\[ \frac {60}{40} = 1,5 \] En vekstfaktor på 1,5 tilsvarer 50% økning, altså er bensinstasjonen 50% dyrere enn butikken.

Oppgave 2

5 delt på 20 er mer enn 5 delt på 40, derfor har Senterpartiet hatt størst prosentvis framgang.

Oppgave 3

Proporsjonalitet

En brus koster 30 kr. Du kjøper et antall flasker brus. prisen du betaler blir større jo flere flasker du kjøper. Dersom du ikke kjøper noen, betaler du ingenting. Kostnaden blir slik:

$ K(antall) = 30 \cdot antall $

eller litt enklere

$K(x) =30x$

Grafen til K er en rett linje som går gjennom origo.

( Dersom du har en rett linje som ikke går gjennom origo, er dette ikke grafen til en funksjon som har proporsjonale variable.)

Omvendt proporsjonalitet

Du skal på seilferie i Middelhavet og vil leie seilbåt. Den koster 30000 kr for to uker. Dersom du reiser alene må du betale hele beløpet selv. Dersom dere er flere som deler på kostnaden blir det billigere.

$K(antall) = \frac{30000}{antall}$ eller : $K(x) = \frac{30000}{x}$

Oppgave 4

Vi skal lage to uttrykk som blir $8 \cdot 10^9$

\[ 4 \cdot 10^1 \cdot 2 \cdot 10^8 = 8 \cdot 10^9 \] \[ 1 \cdot 10^6 \cdot 8 \cdot 10^3 = 8 \cdot 10^9 \]

Oppgave 5

\[ 7\cdot 10^9 + 5 \cdot 10^{12} + 3 \cdot 10^{11}= 7000000000 + 5000000000000 + 300000000000 = 5307000000000 = 5,307 \cdot 10^{12} \]

Oppgave 6

a)

Antall små grønne kvadratet

et stort kvadrat som er figurtall gange figurtall
En søyle med antall småkvadrater tilsvarende figurtall
En diagonal med (figurtall +1) småkvadrater

Oversatt til figur nr. 5 :

\[ 5 \cdot 5 + 5 + 6 = 36 \]

Det er 36 små kvadrater i figur nr 5.

b)

For å lage en formel for antall små kvadrater i figur nr. n, kan man bruke tankegangen i a:

\[ A(n) = n^2 + n + (n+1) = n^2 + 2n + 1 \]

Alternativt:

Skyv søylen av kvadrater til høyre opp ved siden av det store kvadratet. Legg "diagonalen" til under det store kvadratet, og man har et nytt kvadrat som har sider ett kvadrat større enn figurtallet:

\[A(n)= (n+1)^2 \]

Begge uttrykkene er de samme.

Oppgave 7

Oppgave 8

a)

\[ G(x)= ax+b \] \[ a= \frac{\Delta y}{\Delta x}= \frac{y_2-y_1}{x_2-x_1}= \frac{270-90}{20-5} = 12 \]

\[ G(x) =12x +b \]

Bruker et av punktene (5, 90) for å finne b:

\[ 90 = 12 \cdot 5 + b \]

\[b = 30 \]

Da blir yttrykket: $G(x) = 12x + 30$

b)

a som er 12kr er prisen per hekto godteri.
b er prisen på tom bøtte, 30 kr.

c)

\[ G(8) = 12 \cdot 8 + 30 = 126 \]

8 hektogram koster 126 kroner.

DEL TO

Oppgave 1

a)

Utfører regresjonen og får K(x):

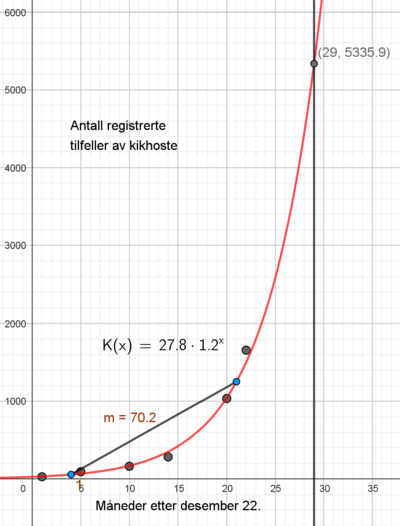
b)

1,2 er vekstfaktoren. Den forteller at økningen er på 20% per år.

c)

Stigningstallet er 70,2. Det betyr at antallet registrete tilfeller i gjennomsnitt øker med 70,2 per måned, i perioden april 23 til september 24.

d)

5336, i følge modellen.

Oppgave 2

a)

Gjennomsnitt per person:

3 300 000km : 40 000personer = 82,5 km/ person

b)

Avstand rundt jorda (omkrets):

3 300 000 km : 83 = 39 759 km

(Denne lengden er ganske riktig i forhold til andre kilder)

Oppgave 3

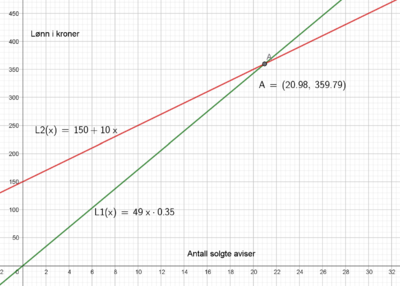
Dersom hun har realistiske forventninger om å selge mer enn 21 aviser, bør hun gå for tilbud 1. Ellers tilbud 2.

Oppgave 4

Vi ser på de forskjellige tilbudene og regner ut full pris ut fra de forskjellige:

$$\frac {99}{4}kr \cdot \frac{100}{51}=48,53 kr$$

Oppgave 5

Oppgave 6

a)

For å fylle inn tabellen trenger vi et uttrykk for høyden. Det er oppgitt at volumet skal være $450 cm^3$.

\[ V = \pi r^2h \] \[ h = \frac{V}{\pi r^2} = \textcolor{red}{\frac{450}{\pi r^2}} \]

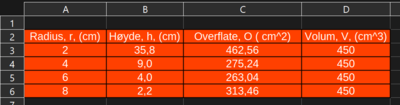
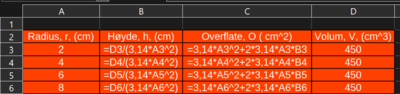
b)

Vi trenger et uttrykk for Overflate og radius:

\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h \]

Her har vi også variabelen h, men den kan vi erstatte med uttrykket fra a:

\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot \textcolor{red}{\frac{450}{\pi r^2}} \]

\[ O(r) = \pi \cdot r^2 + \frac{900}{r } \]

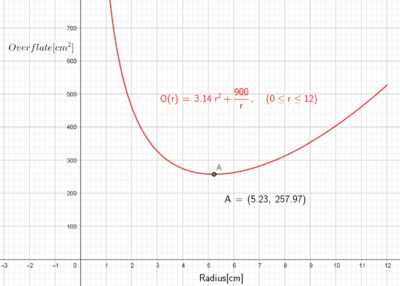
c)

Når radien er 5,23 cm oppnår man den minste overflaten, $257,97cm^2$.

Oppgave 7

Vi forutsetter 20 skoledager per måned. Da blir utgiften til bagett $65 \cdot 20 = 1300$ kroner per måned.

Kostnader ved å lage selv:

20 baguetter 199 kr
4 Crispisalat 80 kr
8 tomater 32,32 kr
Smør 36,90 kr
2pk ost 166,90 kr
2pk skinke 64,60 kr

SUM 579,72kr

Utgiftene blir ca. 580 kr per måned, dersom hun smører bagettene selv. Det betyr at hun sparer 720 kr per måned. Selv om hun "pimper" bagetten opp med ekstra ost og skinke vil hun spare penger.