2P 2025 Vår LØSNING
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
88 % av elevene deltar på undersøkelsen. Det vil si at 100 % - 88 % = 12 % ikke deltar på undersøkelsen
Delen: 3 elever tilsvarer 12 %
Det hele: x tilsvarer 100 %
$\frac{3}{x}=\frac{12}{100}$
$x= \frac{3\cdot 100}{12} = \frac{300}{12}=25$
Det er 25 elever i klassen.
Oppgave 2
a)
Skriver tallene i stigende rekkefølge:
2 2 3 4 4 6 6 7 8 8
Medianen er det midterste tallet, her midt mellom 4 og 6. Medianen er 5.
Gjennomsnitt: $\frac{2 + 2 + 3 + 4 + 4 + 6 + 6 + 7 + 8 + 8}{10}=\frac{50}{10}=5$
b)
Den kumulative frekvensen for 6 personer er 7. Det betyr at 7 vogner i skiheisen hadde 6 eller færre personer om bord.
Oppgave 3
x = vekten til en liten sekk.
y = vekten til en stor sekk.
4 små sekker + 2 store sekker = 44 kg. Dette gir oss likning I:
$4x + 2y=44$
stor sekk = liten sekk + 7 kg. Dette gir oss likning II:
$y = x+7$
Løser likningssystemet ved innsettingsmetoden. Setter x+7 for y i den første likningen.
$4x + 2(x+7)=44$
$4x + 2x+14=44$
$6x=44-14$
$x=\frac{30}{6}$
$x=5$
En liten sekk veier 5 kg. Setter inn denne verdien i den andre likningen.
$y = 5+ 7 = 12$
En stor sekk veier 12 kg.
Oppgave 4
AREAL:
Areal av halvsirkel (en hel sirkel delt på 2): $\frac{\pi r^2}{2} =\frac{\pi \cdot 1^2}{2}=\frac{\pi}{2}\approx\frac{3,14}{2}$
Areal av trekant: $\frac{ g\cdot h}{2}=\frac{3\cdot 1}{2}=\frac{3}{2}$
Arealet av halvsirkelen er litt større enn arealet av trekanten.
OMKRETS:
Omkrets av halvsirkel: $r+r+\frac{2\pi r}{2}=1+1+\frac{2\cdot \pi\cdot 1}{2}=1+1+\pi\approx 5,14$
Omkrets av trekant: $AB+AC+BC=3+AC+BC>6$
Jeg vet ikke nøyaktig hvor lange sidene AC og BC er, men jeg vet at de er like lange, og at de er større enn 1,5. Dette vet jeg fordi trekanten kan deles opp i to rettvinklede trekanter, hvor hypotenusen (AC eller BC) vil være lengre enn den lengste kateten (halvparten av AB).
Omkretsen av trekanten må da være større enn 6, og dette er uansett større enn omkretsen til halvsirkelen.
Oppgave 5
a)
For å finne størrelsen på lånet, legger jeg sammen alle avdragene.
Lånet er $10\cdot 10\,000\,kr=100\,000\,kr$.
b)
Dette er et serielån fordi avdragene er like store. Terminbeløpet er høyest i starten, og går ned etter hvert som lånet nedbetales og man derfor betaler et lavere beløp i rente.
Oppgave 6
GJENNOMSNITT:
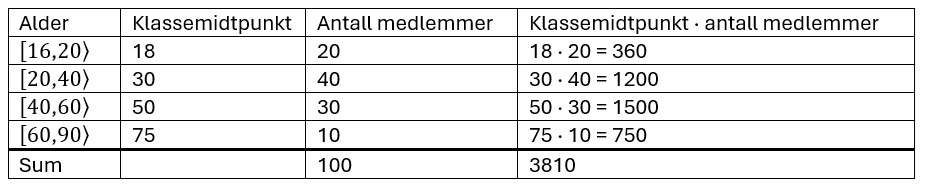
Gjennomsnittsalder: $\frac{3810}{100}=38,1$
Trine har rett i at gjennomsnittsalderen er ca. 38 år. Hun har da antall at personene i hver klasse i gjennomsnitt har alder tilsvarende klassemidtpunktet.
MEDIAN:
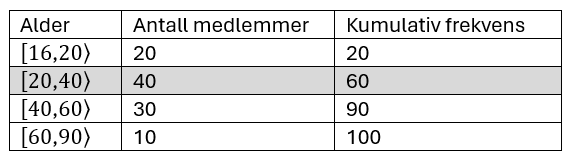
Medianen befinner seg i den klassen person nr. 50 er i, det vil si i klassen 20 til 40 år.
Person nr. 50, som befinner seg 30 personer "inn" i klassen [20,40>.
Vi antar at de 40 medlemmene fordeler seg jevnt i klassen [20,40>. Aldersforskjellen på hver person blir da 20/40=0,5 år. Person nr. 30 i klassen er 0,5*30 = 15 år "inn" i klassen, det vil si at han er 20+15=35 år.
Trine har antatt at personene sin alder fordeler seg jevnt i klassen.