Funksjonen a sin cx + b cos cx
Fra Matematikk.net
Vi ønsker å skrive funksjonen f(x)= a sin cx + b cos cx på formen g(x)= A sin (cx +$\varphi$). Det er alltid mulig.
Altså: a sin cx + b cos cx = A sin (cx + $\varphi$)
$A = \sqrt{a^2 + b^2}$ og $tan \varphi = \frac ba$
NB: $\varphi$ ligger i samme kvadrant som punktet (a, b)
Eksempel
| Eksempel
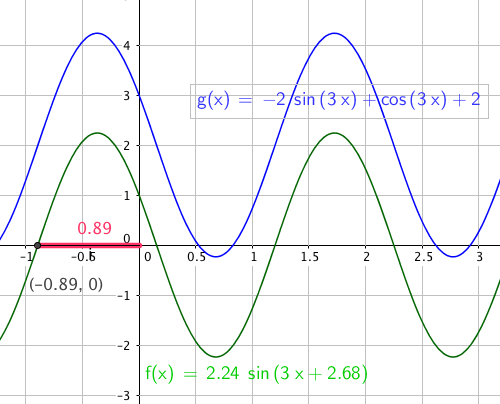
Husk at punktet (-2,1) ligger i andre kvadrant, så vi jakter på en vinkel i denne kvadranten. Vi får : f(x)= 2,24 sin(3x + 2,,678) |
Bevis: