1T 2016 vår LØSNING

Diskusjon av denne oppgaven

Mer diskusjon av denne oppgaven

Løsning av denne oppgaven laget av mattepratbruker LektorH

DEL EN

Oppgave 10

Vi observerer at graf A er den eneste som har et minimum for en negativ x verdi. 2x + 6 = 0 gir løsning for x = - 3, altså er

h(x) funksjonen til graf A.

Graf B har ingen nullpunkter : $b^2 - 4ac < 0$

Vi observerer at $x^2 -2x + 9=0$ ikke har noen løsning, altså er

f(x) funksjonen til graf B.

g(x) er da funksjonen til C.

Oppgave 13

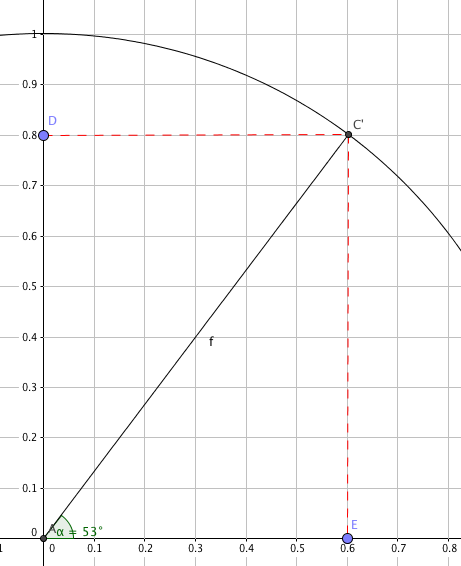
Vi leser av figuren:

$cos 53^{\circ} \approx 0,6 \\ sin 53^{\circ} \approx 0,8$

Tangens:

$tan 53^{\circ} \approx \frac 86 \approx 1,33 $

Oppgave 14

a)

Funksjonen har ekstremalpunkter når den deriverte er null. For x = 0 og x = 4 er det tillfelle. x = 0 er et toppunkt fordi den deriverte skifter fra positiv til negativ verdi, og x = 4 er et bunnpunkt fordi den deriverte skifter fra negativ til positiv verdi.

b)

Likningen for en rett linje er y = ax + b

I punktet (2,-3) er den deriverte lik -2. Det gir y= -2x + b

Setter så punktet (2, -3) inn for x og y for å finne b: $ -3 = -2 \cdot 2 +b$ som gir b=1.

Likningen blir da:

y = -2x + 1