R2 2012 vår LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «<tex>» til «<math>» |
|||
| Linje 11: | Linje 11: | ||
==== 1) ==== | ==== 1) ==== | ||
< | <math> f(x) = 3sin(2x)\\ | ||
u=2x, \quad u' = 2 \\ f'(x) = 2 \cdot 3 cos(2x) \\ f'(x) = 6cos(2x)</tex> | u=2x, \quad u' = 2 \\ f'(x) = 2 \cdot 3 cos(2x) \\ f'(x) = 6cos(2x)</tex> | ||
==== 2) ==== | ==== 2) ==== | ||
< | <math>g(x) = x^2sinx \\ u= x^2, \quad v = sinx \\ g'(x) = 2xsinx + x^2cosx =x(2sinx+xcosx)</tex> | ||
==== 3) ==== | ==== 3) ==== | ||
< | <math>k(x) = 5cos(\frac{\pi}{12}x-2)+7 \\ k'(x) = - \frac{5 \pi}{12} sin( \frac{\pi}{13}x-2)</tex> | ||
=== b) === | === b) === | ||
< | <math>\int xe^{2x}dx = \frac 12 x e^{2x} - \int \frac12 e^{2x}dx \\ = \frac 12 x e^{2x} - \frac 14 e^{2x} +C \\ = \frac 14 e^{2x}(2x-1) + C</tex> | ||
=== c) === | === c) === | ||
< | <math>\int^7_3 \frac{2x}{x^2-4}dx \\ \frac{2x}{x^2+4} = \frac{A}{x-2}+ \frac{B}{x-2} \\ 2x= A(x+2) + B(x-2) \\ x=2 \Rightarrow A = 1 \\ x= -2 \Rightarrow B=1 \\ \int^7_3 \frac{2x}{x^2-4}dx =\int^7_3 \frac{1}{x-2}dx + \int^7_3 \frac {1}{x+2}dx \\ = [ln|x-2|]^7_3 + [ln|x+2|]^7_3 \\ = ln5-ln1+ln9-ln5 = ln3^2 = 2ln3</tex> | ||
=== d) === | === d) === | ||
< | <math> y' -2y = 3 \\ y' \cdot e^{-2x}-2ye^{-2x} = 3e^{-2x} \\ (ye^{-2x})' =3e^{-2x} \\ ye^{-2x} = - \frac 32 e^{-2x} + C \\ y = - \frac 32 +Ce^{2x} \\y(o) = 8 \Rightarrow 8 = - \frac 32 + C \Rightarrow C = \frac{19}{2} \\ y = - \frac 32 + \frac{19}{2}e^{2x}</tex> | ||
=== e) === | === e) === | ||
< | <math>1+e^{-x} + e^{-2x}+ .... \quad x > 0</tex> | ||
==== 1) ==== | ==== 1) ==== | ||
< | <math>k= \frac{e^{-x}}{1} = \frac{e^{-2x}}{e^{-x}} = e^{-x}</tex> | ||
<p></p> < | <p></p> <math> -1 < e^{-x}<1 </tex> | ||
Dvs: rekken konvergerer. | Dvs: rekken konvergerer. | ||
==== 2) ==== | ==== 2) ==== | ||
< | <math>S = \frac{a_1}{1-k} = \frac{1}{1-e^{-x}} = \frac {e^x}{e^x -1}</tex> | ||
| Linje 51: | Linje 51: | ||
== Oppgave 3 == | == Oppgave 3 == | ||
< | <math>f(x) = x \cdot e^x</tex> | ||
=== a) === | === a) === | ||
< | <math>f'(x) = e^x +xe^x = (x+1)e^x \\ f''(x) = e^x + (x+1)e^x = (x+2)e^x </tex> | ||
=== b) === | === b) === | ||
=== c) === | === c) === | ||
< | <math> f^{(n)} (x) = (x+n) e^x \\ n = 1: \quad f'(x) = e^x + xe^x = (1+x)e^x</tex><p></p> Formelen stemmer for n = 1.<p></p> | ||
Setter n = k og undersøker om formelen stemmer for k + 1: <p></p> | Setter n = k og undersøker om formelen stemmer for k + 1: <p></p> | ||
< | <math>f^{(k+1)} = ((x+k)e^x)' = (x+k)'e^x + (x+k)(e^x)' = (x+k+1)e^x</tex> <p></p> | ||
Man slutter av dette at formelen gjelder for alle naturlige tall. | Man slutter av dette at formelen gjelder for alle naturlige tall. | ||
| Linje 71: | Linje 71: | ||
== Oppgave 4 == | == Oppgave 4 == | ||
=== a) === | === a) === | ||
< | <math> f(t) = 19 -4cos(\frac{\pi \cdot t}{180}) \\ f(85) = 19 -4cos(\frac{\pi \cdot 85}{180}) = 18,65 </tex> | ||
<p></p> Det begynner å mørkne kl. 18:39 på kvelden den 25. mars, i følge modellen. | <p></p> Det begynner å mørkne kl. 18:39 på kvelden den 25. mars, i følge modellen. | ||
Definerer 1. januar som dag 1. (kan også definere den som dag 0) | Definerer 1. januar som dag 1. (kan også definere den som dag 0) | ||
| Linje 85: | Linje 85: | ||
Dette kan leses direkte fra grafen. Man observerer at det er to løsninger. Man kan også regne det ut: | Dette kan leses direkte fra grafen. Man observerer at det er to løsninger. Man kan også regne det ut: | ||
<p></p> | <p></p> | ||
< | <math> f(t) = 18 \\ 19 - 4cos( \frac{\pi \cdot t}{180}) = 18 \\ t=76 \quad \vee \quad t= 256</tex> | ||
<p></p> | <p></p> | ||
Lyset slåes på kl. 18:00 16 mars og 16 september. | Lyset slåes på kl. 18:00 16 mars og 16 september. | ||
| Linje 96: | Linje 96: | ||
< | <math> tan(u-v) = \frac{sin(u-v)}{cos(u-v)}\\ = \frac{sin u \cdot cos v - cos u\cdot sinv }{cos u \cdot cos v + sin u \cdot sin v} \\ = \frac{ \frac {sin u \cdot cos v}{cos u \cdot cos v} - \frac {cos u \cdot sinv}{cos u \cdot cos v} }{ \frac {cos u \cdot cos v}{cos u \cdot cos v} + \frac{sin u \cdot sin v}{cos u \cdot cos v}} \\ = \frac{tan u - tan v}{1 - tan u \cdot tan v}</tex> | ||
=== b) === | === b) === | ||
< | <math> f(x) = tan( \alpha) = tan (u - v) = \frac{tan u - tan v}{1 - tan u \cdot tan v} \\ = \frac{ \frac 4x - \frac 1x}{1 + \frac 4x \cdot \frac 1x} = \frac{4x-x}{x^2 + 4} = \frac{3x}{x^2 +4}</tex> | ||
=== c) === | === c) === | ||
< | <math>f'(x)= \frac{3(x^2+4)-3x \cdot 2x}{ (x^2+4)^2} = \frac{12-3x^2}{(x^2+4)^2} \\ f'(x)= 0 \Rightarrow 12-3x^2=0 \\ x= 2 | ||
\\ f(2) = \frac 34</tex> | \\ f(2) = \frac 34</tex> | ||
=== d) === | === d) === | ||
største synsvinkel:<p></p> | største synsvinkel:<p></p> | ||
< | <math>\frac 34 =tan( \alpha) \\ \alpha = 36,9^{\circ}</tex> | ||
== Oppgave 6 == | == Oppgave 6 == | ||
| Linje 113: | Linje 113: | ||
=== a) === | === a) === | ||
< | <math>v_0 = 25m/s \\ y- fart \\y' - akslerasjon \\ \\ y' = ky^2 \\ Bestemmer \quad k: \\ | ||
-12 = k \cdot25^2 \\ k = 0,02 \\ \\ \frac{dy}{dx} = -0,02y^2 \\ \int{y^{-2}}dy = \int -0,02dx \\ -y^{-1}= -0,02x + c \\ y= \frac{1}{0,02x+c}</tex> | -12 = k \cdot25^2 \\ k = 0,02 \\ \\ \frac{dy}{dx} = -0,02y^2 \\ \int{y^{-2}}dy = \int -0,02dx \\ -y^{-1}= -0,02x + c \\ y= \frac{1}{0,02x+c}</tex> | ||
| Linje 119: | Linje 119: | ||
Ved tiden x = 0:<p></p> | Ved tiden x = 0:<p></p> | ||
< | <math>y = \frac 1C \\ 25 = \frac 1C \\ c = 0,04 </tex> | ||
<p></p> | <p></p> | ||
Farten til båten ved x = 3:<p></p> | Farten til båten ved x = 3:<p></p> | ||
< | <math>y(3) = \frac {1}{0,06 + 0,04} = 10 m/s</tex> | ||
=== c) === | === c) === | ||
Sideversjonen fra 5. feb. 2013 kl. 20:57
DEL EN
Oppgave 1
a)
1)
<math> f(x) = 3sin(2x)\\ u=2x, \quad u' = 2 \\ f'(x) = 2 \cdot 3 cos(2x) \\ f'(x) = 6cos(2x)</tex>
2)
<math>g(x) = x^2sinx \\ u= x^2, \quad v = sinx \\ g'(x) = 2xsinx + x^2cosx =x(2sinx+xcosx)</tex>
3)
<math>k(x) = 5cos(\frac{\pi}{12}x-2)+7 \\ k'(x) = - \frac{5 \pi}{12} sin( \frac{\pi}{13}x-2)</tex>
b)
<math>\int xe^{2x}dx = \frac 12 x e^{2x} - \int \frac12 e^{2x}dx \\ = \frac 12 x e^{2x} - \frac 14 e^{2x} +C \\ = \frac 14 e^{2x}(2x-1) + C</tex>
c)
<math>\int^7_3 \frac{2x}{x^2-4}dx \\ \frac{2x}{x^2+4} = \frac{A}{x-2}+ \frac{B}{x-2} \\ 2x= A(x+2) + B(x-2) \\ x=2 \Rightarrow A = 1 \\ x= -2 \Rightarrow B=1 \\ \int^7_3 \frac{2x}{x^2-4}dx =\int^7_3 \frac{1}{x-2}dx + \int^7_3 \frac {1}{x+2}dx \\ = [ln|x-2|]^7_3 + [ln|x+2|]^7_3 \\ = ln5-ln1+ln9-ln5 = ln3^2 = 2ln3</tex>
d)
<math> y' -2y = 3 \\ y' \cdot e^{-2x}-2ye^{-2x} = 3e^{-2x} \\ (ye^{-2x})' =3e^{-2x} \\ ye^{-2x} = - \frac 32 e^{-2x} + C \\ y = - \frac 32 +Ce^{2x} \\y(o) = 8 \Rightarrow 8 = - \frac 32 + C \Rightarrow C = \frac{19}{2} \\ y = - \frac 32 + \frac{19}{2}e^{2x}</tex>
e)
<math>1+e^{-x} + e^{-2x}+ .... \quad x > 0</tex>
1)
<math>k= \frac{e^{-x}}{1} = \frac{e^{-2x}}{e^{-x}} = e^{-x}</tex>
<math> -1 < e^{-x}<1 </tex>
Dvs: rekken konvergerer.
2)
<math>S = \frac{a_1}{1-k} = \frac{1}{1-e^{-x}} = \frac {e^x}{e^x -1}</tex>
Oppgave 2
a)
b)
c)
Oppgave 3
<math>f(x) = x \cdot e^x</tex>
a)
<math>f'(x) = e^x +xe^x = (x+1)e^x \\ f(x) = e^x + (x+1)e^x = (x+2)e^x </tex>
b)
c)
<math> f^{(n)} (x) = (x+n) e^x \\ n = 1: \quad f'(x) = e^x + xe^x = (1+x)e^x</tex>
Formelen stemmer for n = 1.
Setter n = k og undersøker om formelen stemmer for k + 1:
<math>f^{(k+1)} = ((x+k)e^x)' = (x+k)'e^x + (x+k)(e^x)' = (x+k+1)e^x</tex>
Man slutter av dette at formelen gjelder for alle naturlige tall.
DEL TO
Oppgave 4
a)
<math> f(t) = 19 -4cos(\frac{\pi \cdot t}{180}) \\ f(85) = 19 -4cos(\frac{\pi \cdot 85}{180}) = 18,65 </tex>
Det begynner å mørkne kl. 18:39 på kvelden den 25. mars, i følge modellen.
Definerer 1. januar som dag 1. (kan også definere den som dag 0)
b)
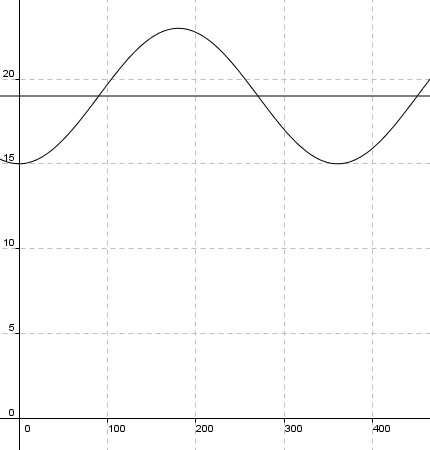
Likevektslinjen er 19.
Amplitude: Den største verdi f kan ha er 23, da er amplituden 4. Det kan leses fra funksjonsuttrykket, absoluttverdien av faktoren i "cosinus" leddet.
Perioden er 360.
Det gjennomsnittlige tidspunkt når lyset slåes på, gjennom hele året, er kl. 19:00.
c)
Dette kan leses direkte fra grafen. Man observerer at det er to løsninger. Man kan også regne det ut:
<math> f(t) = 18 \\ 19 - 4cos( \frac{\pi \cdot t}{180}) = 18 \\ t=76 \quad \vee \quad t= 256</tex>
Lyset slåes på kl. 18:00 16 mars og 16 september.
d)
Oppgave 5
a)
<math> tan(u-v) = \frac{sin(u-v)}{cos(u-v)}\\ = \frac{sin u \cdot cos v - cos u\cdot sinv }{cos u \cdot cos v + sin u \cdot sin v} \\ = \frac{ \frac {sin u \cdot cos v}{cos u \cdot cos v} - \frac {cos u \cdot sinv}{cos u \cdot cos v} }{ \frac {cos u \cdot cos v}{cos u \cdot cos v} + \frac{sin u \cdot sin v}{cos u \cdot cos v}} \\ = \frac{tan u - tan v}{1 - tan u \cdot tan v}</tex>
b)
<math> f(x) = tan( \alpha) = tan (u - v) = \frac{tan u - tan v}{1 - tan u \cdot tan v} \\ = \frac{ \frac 4x - \frac 1x}{1 + \frac 4x \cdot \frac 1x} = \frac{4x-x}{x^2 + 4} = \frac{3x}{x^2 +4}</tex>
c)
<math>f'(x)= \frac{3(x^2+4)-3x \cdot 2x}{ (x^2+4)^2} = \frac{12-3x^2}{(x^2+4)^2} \\ f'(x)= 0 \Rightarrow 12-3x^2=0 \\ x= 2 \\ f(2) = \frac 34</tex>
d)
største synsvinkel:
<math>\frac 34 =tan( \alpha) \\ \alpha = 36,9^{\circ}</tex>
Oppgave 6
a)
<math>v_0 = 25m/s \\ y- fart \\y' - akslerasjon \\ \\ y' = ky^2 \\ Bestemmer \quad k: \\ -12 = k \cdot25^2 \\ k = 0,02 \\ \\ \frac{dy}{dx} = -0,02y^2 \\ \int{y^{-2}}dy = \int -0,02dx \\ -y^{-1}= -0,02x + c \\ y= \frac{1}{0,02x+c}</tex>
b)
Ved tiden x = 0:
<math>y = \frac 1C \\ 25 = \frac 1C \\ c = 0,04 </tex>
Farten til båten ved x = 3:
<math>y(3) = \frac {1}{0,06 + 0,04} = 10 m/s</tex>
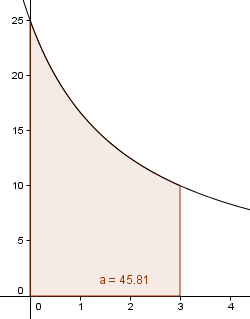
c)
Båten har forflyttet seg ca. 46 meter på 3 sekunder.