Periodiske funksjoner: Forskjell mellom sideversjoner
Fra Matematikk.net
Ingen redigeringsforklaring |
m Teksterstatting – «<tex>» til «<math>» |
||
| Linje 1: | Linje 1: | ||
En periodisk funksjon < | En periodisk funksjon <math>f(x)</tex> på et intervall <math>I</tex> med periode <math>d</tex> er kjennetegnet ved at <math>f(x+d)=f(x) \, \forall x \in I</tex> (gitt at <math>x+d\in I</tex>). Da vil også <math>f(x+nd)=f(x) \, \forall n \in \mathbb{Z}</tex>. | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
| Linje 5: | Linje 5: | ||
'''Eksempel''' | '''Eksempel''' | ||
:< | :<math>f(x)=\sin(x)</tex> på <math>\mathbb{R}</tex> med periode <math>d=2\pi</tex>. Det er evident at <math>\sin(x)=\sin(x+2\pi)\,\forall x \in \mathbb{R}</tex>. Vi sier gjerne at <math>\sin(x)</tex> er <math>2\pi</tex> -periodisk eller at bølgelengden er <math>2\pi</tex>. | ||
</blockquote> | </blockquote> | ||
| Linje 14: | Linje 14: | ||
'''Bevis''' | '''Bevis''' | ||
:La < | :La <math>f(x)</tex> og <math>g(x)</tex> være to funksjoner med periode <math>d</tex> definert på den reelle tallinja. Da er <math>f(x+d)=f(x)</tex> og <math>g(x+d)=g(x)</tex> for alle reelle <math>x</tex>. Hvis vi legger sammen funksjonene og definerer <math>h(x)=f(x)+g(x)</tex>, ser vi at <math>h(x+d)=f(x+d)+g(x+d)=f(x)+g(x)=h(x)</tex>, så <math>h(x)</tex> har egenskapen til en periodisk funksjon. | ||
</blockquote> | </blockquote> | ||
Perioden til en gitt funksjon < | Perioden til en gitt funksjon <math>f(x)</tex> er den minste verdien av <math>d</tex> slik at <math>f(x+d)=f(x)\,\forall x</tex>. | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
| Linje 24: | Linje 24: | ||
'''Eksempel''' | '''Eksempel''' | ||
:Ser vi på produktet < | :Ser vi på produktet <math>f(x)=\sin(x)\cos(x)</tex> vil <math>f(x+2\pi)=f(x)</tex>, men funksjonen vil også oppfylle <math>f(x+\pi)=f(x)</tex>, så perioden til funksjonen vil være <math>d=\pi</tex>. Dette er altså en liten fallgrube siden det kanskje kan være fristende å konkludere med at perioden til produktet av to <math>2\pi</tex> -periodiske funksjoner har periode <math>2\pi</tex>. | ||
</blockquote> | </blockquote> | ||
| Linje 33: | Linje 33: | ||
[[Bilde:periodisk1.png|right|thumb|Periodisk utvidelse av f(x)=x]] | [[Bilde:periodisk1.png|right|thumb|Periodisk utvidelse av f(x)=x]] | ||
Vi kan konstruere periodiske funksjoner på f.eks. < | Vi kan konstruere periodiske funksjoner på f.eks. <math>\mathbb{R}</tex> ved å utvide en funksjon definert på et begrenset intervall. | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
| Linje 39: | Linje 39: | ||
'''Eksempel''' | '''Eksempel''' | ||
: Ser vi på restriksjonen av < | : Ser vi på restriksjonen av <math>f(x)=x</tex> på intervallet <math>\langle 0,1]</tex> kan vi utvide denne til en periodisk funksjon på hele <math>\mathbb{R}</tex> gjennom å kreve at <math>f(x+1)=f(x) \, \forall x\in\mathbb{R}</tex>. Det vi har gjort er å utvide domenet til funksjonen fra det halvåpne intervallet <math>\langle 0,1]</tex> til hele den reelle tallinja på en slik måte at <math>f:\mathbb{R}\to\mathbb{R}</tex> blir periodisk. | ||
</blockquote> | </blockquote> | ||
Sideversjonen fra 5. feb. 2013 kl. 20:57
En periodisk funksjon <math>f(x)</tex> på et intervall <math>I</tex> med periode <math>d</tex> er kjennetegnet ved at <math>f(x+d)=f(x) \, \forall x \in I</tex> (gitt at <math>x+d\in I</tex>). Da vil også <math>f(x+nd)=f(x) \, \forall n \in \mathbb{Z}</tex>.
Eksempel
- <math>f(x)=\sin(x)</tex> på <math>\mathbb{R}</tex> med periode <math>d=2\pi</tex>. Det er evident at <math>\sin(x)=\sin(x+2\pi)\,\forall x \in \mathbb{R}</tex>. Vi sier gjerne at <math>\sin(x)</tex> er <math>2\pi</tex> -periodisk eller at bølgelengden er <math>2\pi</tex>.
Enhver sum av funksjoner med lik periode er selv periodisk med samme periode.
Bevis
- La <math>f(x)</tex> og <math>g(x)</tex> være to funksjoner med periode <math>d</tex> definert på den reelle tallinja. Da er <math>f(x+d)=f(x)</tex> og <math>g(x+d)=g(x)</tex> for alle reelle <math>x</tex>. Hvis vi legger sammen funksjonene og definerer <math>h(x)=f(x)+g(x)</tex>, ser vi at <math>h(x+d)=f(x+d)+g(x+d)=f(x)+g(x)=h(x)</tex>, så <math>h(x)</tex> har egenskapen til en periodisk funksjon.
Perioden til en gitt funksjon <math>f(x)</tex> er den minste verdien av <math>d</tex> slik at <math>f(x+d)=f(x)\,\forall x</tex>.
Eksempel
- Ser vi på produktet <math>f(x)=\sin(x)\cos(x)</tex> vil <math>f(x+2\pi)=f(x)</tex>, men funksjonen vil også oppfylle <math>f(x+\pi)=f(x)</tex>, så perioden til funksjonen vil være <math>d=\pi</tex>. Dette er altså en liten fallgrube siden det kanskje kan være fristende å konkludere med at perioden til produktet av to <math>2\pi</tex> -periodiske funksjoner har periode <math>2\pi</tex>.
Periodisk utvidelse
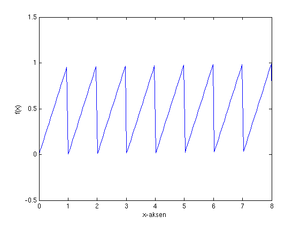
Vi kan konstruere periodiske funksjoner på f.eks. <math>\mathbb{R}</tex> ved å utvide en funksjon definert på et begrenset intervall.
Eksempel
- Ser vi på restriksjonen av <math>f(x)=x</tex> på intervallet <math>\langle 0,1]</tex> kan vi utvide denne til en periodisk funksjon på hele <math>\mathbb{R}</tex> gjennom å kreve at <math>f(x+1)=f(x) \, \forall x\in\mathbb{R}</tex>. Det vi har gjort er å utvide domenet til funksjonen fra det halvåpne intervallet <math>\langle 0,1]</tex> til hele den reelle tallinja på en slik måte at <math>f:\mathbb{R}\to\mathbb{R}</tex> blir periodisk.