Løsning del 2 utrinn Vår 11

Oppgave 1

a)

Pris i 2010: <tex>26990kr \cdot 1,12 = 30229kr</tex>

b)

<tex>v = \frac st \Rightarrow t = \frac sv = \frac{10km}{30 km/t} = \frac 13 time = 20 minutter.</tex>

C)

600km = 60 mil, og den bruker 0,2 l/mil:

<tex> 60mil \cdot 0,2 l/mil = 12 liter </tex>

Oppgave 2

a)

Når man skal sammenligne størrelsen på brøker er det lettest om gjør om til felles nevner. I dette tilfellet er det lurt å gjøre om til en brøk med nevner lik 32:

<tex> \frac 38 = \frac {12}{32}, \quad \frac {15}{32},\quad \frac {1}{2}=\frac {16}{32}, \quad \frac {19}{32},\quad \frac {11}{16}= \frac {22}{32}, \quad \frac {3}{4}= \frac {24}{32} </tex>

b)

Her må man huske at diameter er to ganger radius:

<tex> V= \pi r^2h = 3,14 \cdot (2,6cm)^2 \cdot 5,78cm = 122,75cm^2</tex>

c)

Maksimum radius: <tex> V= \pi r^2h \Rightarrow r = \sqrt{\frac {V}{\pi h} } =\sqrt{\frac {125,0 cm^3}{3,14 \cdot 5,78 cm} } = 2,6247cm </tex>

Maksimum diameter blir da 2r som er 5,25cm eller 52,5 mm

Oppgave 5

a)

Leser fra graf: Peder var i Ås fra 18:15 til 19:00, dvs. 45 minutter.

b)

Leser av graf: Køen begynte 30km fra Sarpsborg.

c)

Turen tok 1 time og 15 minutter som er 1,25 timer. Strekningen var 60km.

<tex> v= \frac st \Rightarrow v = \frac{60km}{1,25t}= 48 km/t</tex>

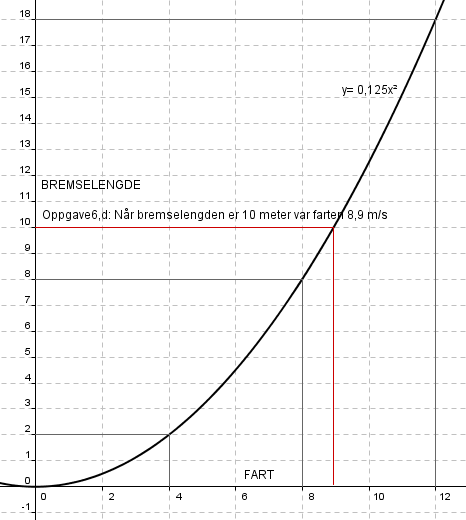
Oppgave 6

a)

Fart = 8,0 m/s gir bremselengde 2 ganger 4 meter, dvs. 8m.

Fart = 12,0 m/s gir bremselengde 2 ganger 9 meter, dvs. 18m.

b)

<tex>y = k \cdot x^2 \Rightarrow k = \frac{y}{x^2}</tex>

Setter inn x = 4,0 og y = 2,0 og får:

<tex>k = \frac{2,0}{4,0^2} = \frac {2}{18} = \frac 18 = 0,125</tex>

c)

d) Se figur i c for grafisk løsning. Ved regning:

<tex>y = k \cdot x^2 \Rightarrow 10,0 = 0,125 \cdot x^2 \Rightarrow x = \sqrt{\frac{10}{0,125}}=8,9</tex>

Farten må ha vært 8,9 m/s når bremselengden er 10 meter.

Oppgave 7

a)

Areal: <tex>A = (230m)^2 = 52900m^2</tex>

Omkrets: <tex>O = 4 \cdot 230m = 920m</tex>

b)

Formlike trekanter:

<tex>\frac {2}{7,5} = \frac{h}{546} \Rightarrow h = 145,6</tex>

c)Volum av pyramide:

<tex>V = \frac 13Gh = \frac13 \cdot 52900m^2 \cdot 145,6m = 2567387,7 m^3</tex>

Volumet er ca 2,57 milioner kubikkmeter.

Oppgave 9

Trekanten ABC er formlik med trekanten CDE.

<tex> \frac{x}{x+30} = \frac {45}{50} \Rightarrow x =270</tex>

Skipet er 270 meter fra land.