Fortegnsskjema: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Et fortegnsskjema kan være nyttig i flere sammenhenger, som for eksempel ved drøfting av funksjoner eller ved løsing av ulikheter. '''Eks:''' Vi har ulikheten: Fra fortegnsskjemae... |
Ingen redigeringsforklaring |
||
| Linje 5: | Linje 5: | ||
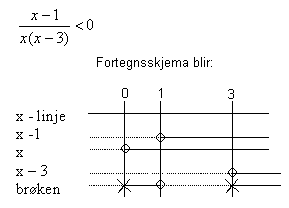
Vi har ulikheten: | Vi har ulikheten: | ||
[[Bilde:Fortegnsskjema.gif]] | |||
Fra fortegnsskjemaet ser man hvor brøkens faktorer er negative og positive og man kan lese direkte fra skjemaet for hvilke x verdier ulikheten er oppfylt. Stiplet linje representerer negative verdier og heltrukket linje positive verdier. | Fra fortegnsskjemaet ser man hvor brøkens faktorer er negative og positive og man kan lese direkte fra skjemaet for hvilke x verdier ulikheten er oppfylt. Stiplet linje representerer negative verdier og heltrukket linje positive verdier. | ||
Sideversjonen fra 15. aug. 2011 kl. 04:48
Et fortegnsskjema kan være nyttig i flere sammenhenger, som for eksempel ved drøfting av funksjoner eller ved løsing av ulikheter.
Eks:
Vi har ulikheten:
Fra fortegnsskjemaet ser man hvor brøkens faktorer er negative og positive og man kan lese direkte fra skjemaet for hvilke x verdier ulikheten er oppfylt. Stiplet linje representerer negative verdier og heltrukket linje positive verdier.
På samme måte kan man trekke opp skjema for funksjoner og deriverte for å få oversikt over funksjonens oppførsel.