Pyramide: Forskjell mellom sideversjoner
Ny side: En pyramide er en romfigur dannet ved at man har et polygon (grunnflaten) og et punkt som ikke ligger i grunnflatens plan. Når man trekker linjene fra polygones hjørner til punktet (toppu... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
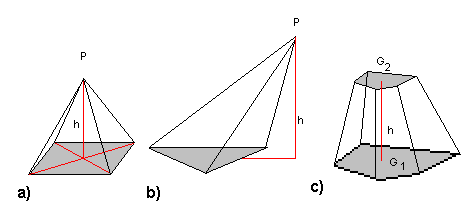
En pyramide er en romfigur dannet ved at man har et polygon (grunnflaten) og et punkt som ikke ligger i grunnflatens plan. Når man trekker linjene fra polygones hjørner til punktet (toppunktet) dannes pyramiden. Pyramidene har ofte navn etter hvor mange sider de har, altså antall sider i polygone. Nedenfor vises en regulær firkantet pyramide. Pyramiden er regulær fordi loddlinja fra toppunktet treffer midt i grunnflaten, og fordi grunnflaten er et regulært polygon. Figuren i b viser en trekantet ikke-regulær pyramide. Figur c viser en pyramidestump. | En pyramide er en romfigur dannet ved at man har et polygon (grunnflaten) og et punkt som ikke ligger i grunnflatens plan. Når man trekker linjene fra polygones hjørner til punktet (toppunktet) dannes pyramiden. Pyramidene har ofte navn etter hvor mange sider de har, altså antall sider i polygone. Nedenfor vises en regulær firkantet pyramide. Pyramiden er regulær fordi loddlinja fra toppunktet treffer midt i grunnflaten, og fordi grunnflaten er et regulært polygon. Figuren i b viser en trekantet ikke-regulær pyramide. Figur c viser en pyramidestump. | ||
[[Bilde:Pyramide.gif]] | |||
Volumet av en pyramide er gitt ved: | Volumet av en pyramide er gitt ved: | ||
Sideversjonen fra 31. jul. 2011 kl. 15:49
En pyramide er en romfigur dannet ved at man har et polygon (grunnflaten) og et punkt som ikke ligger i grunnflatens plan. Når man trekker linjene fra polygones hjørner til punktet (toppunktet) dannes pyramiden. Pyramidene har ofte navn etter hvor mange sider de har, altså antall sider i polygone. Nedenfor vises en regulær firkantet pyramide. Pyramiden er regulær fordi loddlinja fra toppunktet treffer midt i grunnflaten, og fordi grunnflaten er et regulært polygon. Figuren i b viser en trekantet ikke-regulær pyramide. Figur c viser en pyramidestump.
Volumet av en pyramide er gitt ved:
V = (1/3)Gh , der G er grunnflaten av pyramiden og h er høyden.
Volumet av en pyramidestump er gitt ved:
V = (h/3)(G1 + √G1G2 + G2)
(det midterste leddet i den andre parentesen er kvadratroten av produktet av flatene)