Enhetsvektor: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Vektor med lengde en i et ortonormert koordinatsystem. Notasjonen er ofte ex,ey, ez. Bokstaven e kan i enkelte bøker ha en pil pekende mot høyre over seg. Når vi i rommet refererer t... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
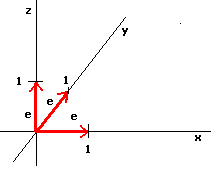
Vektor med lengde en i et ortonormert koordinatsystem. Notasjonen er ofte ex,ey, ez. Bokstaven e kan i enkelte bøker ha en pil pekende mot høyre over seg. | Vektor med lengde en i et ortonormert koordinatsystem. Notasjonen er ofte ex,ey, ez. Bokstaven e kan i enkelte bøker ha en pil pekende mot høyre over seg. | ||
[[Bilde:Enhetsvektor.gif]] | |||
Når vi i rommet refererer til vektoren [1,2,3] refererer vi egentlig til [1 | Når vi i rommet refererer til vektoren [1,2,3] refererer vi egentlig til <tex>[1 \cdot \vec{e_x}, 2 \cdot \vec{e_y}, , 3 \cdot \vec{e_z}, ]</tex>, men for å spare tid og å gjøre notasjonen enklere skriver vi bare [1,2,3]. | ||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Sideversjonen fra 8. jul. 2011 kl. 17:32
Vektor med lengde en i et ortonormert koordinatsystem. Notasjonen er ofte ex,ey, ez. Bokstaven e kan i enkelte bøker ha en pil pekende mot høyre over seg.
Når vi i rommet refererer til vektoren [1,2,3] refererer vi egentlig til <tex>[1 \cdot \vec{e_x}, 2 \cdot \vec{e_y}, , 3 \cdot \vec{e_z}, ]</tex>, men for å spare tid og å gjøre notasjonen enklere skriver vi bare [1,2,3].