Løsning del 2 utrinn VÅR 09: Forskjell mellom sideversjoner
Fra Matematikk.net
| Linje 4: | Linje 4: | ||
== Oppgave 4 == | == Oppgave 4 == | ||
[[Bilde:4.2009.png]] | [[Bilde:4.2009.png]] | ||
<p></p> | |||
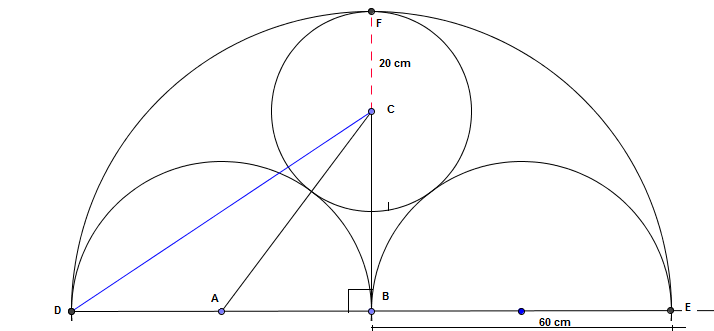
a) BC er 40 cm fordi CF er 20 cm og radien BE = BF = 60cm.<p></p> | |||
b)Pytagoras gir oss <tex>(AC)^2 = \sqrt{(AB)^2+(BC)^2}= \sqrt{900+1600}=50cm </tex> | |||
== Oppgave 5 == | == Oppgave 5 == | ||
Sideversjonen fra 20. apr. 2011 kl. 20:25
Oppgave 1
Oppgave 2
Oppgave 3
Oppgave 4
a) BC er 40 cm fordi CF er 20 cm og radien BE = BF = 60cm.
b)Pytagoras gir oss <tex>(AC)^2 = \sqrt{(AB)^2+(BC)^2}= \sqrt{900+1600}=50cm </tex>
Oppgave 5
r = 5cm
a) Volum av sylinder: <tex> V_s = \pi r^2h = \pi r^22r = 2 \pi r^3 = 785 cm^3</tex>
b) Volumet av kule: <tex> V_k = \frac43 \pi r^3 = 523 cm^3</tex>
c) <tex> \frac {V_k}{V_s} = \frac{\frac43 \pi r^3}{2 \pi r^3}= \frac{4}{3 \cdot 2} = \frac {2}{3}</tex>
Som skulle vises.
Oppgave 6
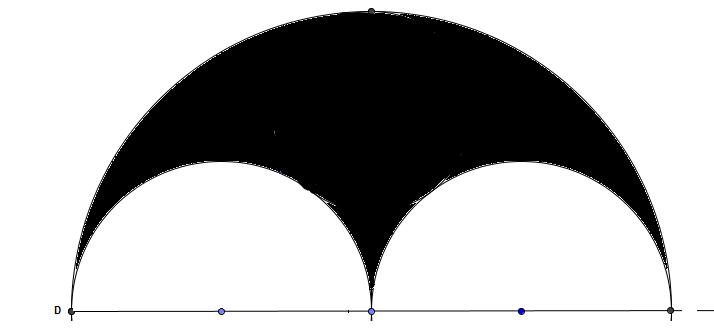
Vi har tre halvsirkler. Den store halvsirkelen har radius 10cm. De to små har radius 5cm.