Ulikheter: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 1: | Linje 1: | ||
== Innledning == | == Innledning == | ||
| Linje 41: | Linje 40: | ||
Ulikheter der deler av x (i første) inngår løses som en ligning. Alle ledd med x samles på venstre side og trekkes sammen, og alle tall samles på høyre side og trekkes sammen. | Ulikheter der deler av x (i første) inngår løses som en ligning. Alle ledd med x samles på venstre side og trekkes sammen, og alle tall samles på høyre side og trekkes sammen. | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
Eks 2: | '''Eks 2:''' | ||
4x -2 > 10 – 2x | 4x -2 > 10 – 2x | ||
| Linje 56: | Linje 56: | ||
I eksempel 2 har vi kun brukt de samme reglene som gjelder for behandling av ligninger. | I eksempel 2 har vi kun brukt de samme reglene som gjelder for behandling av ligninger. | ||
</blockquote> | |||
Legg merke til at det er uendelig mange x verdier som passer i ulikhetene i eksempel 2 og 3. | Legg merke til at det er uendelig mange x verdier som passer i ulikhetene i eksempel 2 og 3. | ||
Sideversjonen fra 23. jan. 2011 kl. 13:33
Innledning
Ulikhetstegnene < og > brukes til å fortelle at en størrelse er mindre eller større enn en annen.
x > y leses ”x er større enn y”
x < y leses ” x er mindre enn y”
I tillegg har man tegnene ≥ som leses "...større eller lik..... ", og som leses "...mindre eller lik...".
Ulikheter løses som ligninger med et viktig unntak:
Dersom man multipliserer eller dividerer hvert ledd i en ulikhet med samme negative tall, må ulikhetstegnet snus.
Eks 1:
4 > 2
Usagnet forteller oss at fire er større enn to, noe som er riktig ut fra vår forestiling om tallenes verdi. Dersom vi multipliserer utrykket med -1 får vi:
-4 < -2Vi har snudd ulikhetstegnet og observerer at utsagnet er riktig fordi -4 er mindre enn -2.
Enkle ulikheter
Ulikheter der deler av x (i første) inngår løses som en ligning. Alle ledd med x samles på venstre side og trekkes sammen, og alle tall samles på høyre side og trekkes sammen.
Eks 2:
4x -2 > 10 – 2x
4x +2x > 10 + 2
6x > 12
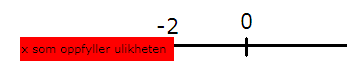
x > 2
I eksempel 2 har vi kun brukt de samme reglene som gjelder for behandling av ligninger.
Legg merke til at det er uendelig mange x verdier som passer i ulikhetene i eksempel 2 og 3.