S1 2025 Vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på Matteprat

Løsningsforslag laget av Håvard Myge NB: liten regnefeil på oppgave 5b, og dermed også 5c.

Del 1

Oppgave 1

Vi skal derivere funksjonen:

$$ f(x) = e^{-2x} + \frac{1}{5}x^5 - 2\pi $$

Deriver ledd for ledd:

• $e^{-2x} \rightarrow -2e^{-2x}$
• $\frac{1}{5}x^5 \rightarrow x^4$
• $-2\pi \rightarrow 0$, siden $\pi$ er konstant.

Svar: $$ \underline{\underline{f'(x) = -2e^{-2x} + x^4}} $$

Oppgave 2

Funksjonen er gitt som:

$$ g(x) = \frac{1}{2} e^x (2x - 1)^2 $$

a)

Vi setter $g(x) = 0$:

$$ \frac{1}{2} e^x (2x - 1)^2 = 0 $$

Siden $e^x \neq 0$, må:

$$ (2x - 1)^2 = 0 \Rightarrow x = \frac{1}{2} $$

Nullpunkt: $\underline{\underline{x = \frac{1}{2}}}$

b)

La:

• $u(x) = \frac{1}{2} e^x$

• $v(x) = (2x - 1)^2$

Da:

$$ g'(x) = u'(x)v(x) + u(x)v'(x) $$ $$ = \frac{1}{2} e^x (2x - 1)^2 + \frac{1}{2} e^x \cdot 2(2x - 1) \cdot 2 $$

$$ = \frac{1}{2} e^x \left( (2x - 1)^2 + 4(2x - 1) \right) $$

Utvid og faktoriser uttrykket:

$$ (2x - 1)^2 + 4(2x - 1) = (2x - 1)(2x - 1 + 4) = (2x - 1)(2x + 3) $$

Vi har vist at: $$ g'(x) = \frac{1}{2} e^x (2x - 1)(2x + 3) $$

c)

Finn stasjonære punkter ved å løse $g'(x) = 0$:

$$ \frac{1}{2} e^x (2x - 1)(2x + 3) = 0 $$

Løsning: $x = \frac{1}{2}$ og $x = -\frac{3}{2}$

Finn $g(x)$-verdiene:

• $g\left(\frac{1}{2}\right) = \frac{1}{2} e^{1/2} \cdot 0 = 0$

• $g\left(-\frac{3}{2}\right) = \frac{1}{2} e^{-3/2} \cdot (-4)^2 = \frac{1}{2} e^{-3/2} \cdot 16 = 8e^{-3/2}$

Svar:

• Bunnpunkt: $\underline{\underline{\left(\frac{1}{2}, 0\right)}}$

• Toppunkt: $\underline{\underline{\left(-\frac{3}{2}, 8e^{-3/2} \right)}}$

Oppgave 3

a)

$$ 3^{3x + 2} - 5 = 76$$ $$ 3^{3x + 2} = 81 = 3^4 $$ $$ 3x + 2 = 4 $$ $$ \underline{\underline{x = \frac{2}{3}}} $$

b)

$$ 3 \lg x + 2 \lg x^2 + \lg\left(\frac{1}{x^9}\right) = 2 $$

Bruk logaritmeregler:

• $\lg x^2 = 2 \lg x$

• $\lg \left( \frac{1}{x^9} \right) = \lg(1) - \lg(x^9) = -9 \lg x$

Da får vi:

$$ 3 \lg x + 4 \lg x - 9 \lg x = 2 $$ $$ -2 \lg x = 2 $$ $$ \lg x = -1 $$ $$ x = 10^{-1} = \underline{\underline{0,1=\frac{1}{10}}} $$

Oppgave 4

a)

Direkte innsetting gir:

$$ \frac{3(9 - 3)}{0} = \frac{18}{0} $$

Ikke av typen $\frac{0}{0}$ – som betyr at grenseverdien kan gå mot $+\infty$, $-\infty$ eller være udefinert.

Når $x \to 3^-$:

• Telleren nærmer seg $18$ og nevneren er negativ og nærmer seg $0$

• $\Rightarrow$ Brøken går mot $-\infty$

Når $x \to 3^+$:

• Telleren nærmer seg $18$ og nevneren er positiv og nærmer seg $0$

• $\Rightarrow$ Brøken går mot $+\infty$

Grenseverdien eksisterer ikke.

b)

$$ \lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4} $$

Bruk konjugatsetning med $x-4$: $$ \lim_{x \to 4} \frac{\sqrt{x} - 2}{(\sqrt{x}-2)(\sqrt{ x } + 2)} $$ $$ \lim_{x \to 4} = \frac{1}{\sqrt{x} + 2} $$ $$ =\frac{1}{\sqrt{4} + 2} = \underline{\underline{\frac{1}{4}}} $$

Oppgave 5

a)

Vi antar at det tredje skuddet ikke har skjedd enda.

P(treff på to skudd) = P(treff)*P(treff)

$=0,8 \cdot 0,8 =0,64$

Sannsynligheten for at Arne treffer på de to første skuddene er 0,64.

b)

P(treff på nøyaktig to skudd) = 3*P(treff)*P(treff)*P(ikke treff)

$=3\cdot 0,8 \cdot 0,8 \cdot 0,2 = 0,64\cdot 0,6 =0,384$

Sannsynligheten for at Arne treffer på nøyaktig to av de tre skuddene er 0,384.

c)

P(treff på høyst ett skudd) = P(ikke treff)*P(ikke treff)*P(ikke treff) + 3*P(treff)*P(ikke treff)*P(ikke treff)

$=0,2^3+3\cdot 0,8\cdot 0,2^2 = 0,008+0,096=0,104$

Sannsynligheten for at Arne treffer på høyst ett av de tre skuddene er 0,104.

Oppgave 6

Funksjonene $f$ og $g$ er gitt ved

$$ f(x) = \begin{cases} x^2 + 2, & x < 0 \\ 2e^x, & x \geq 0 \end{cases} $$

og

$$ g(x) = \begin{cases} x^2 + 2, & x < 0 \\ 1, x=0 \\ 2e^x, & x \geq 0 \end{cases} $$

a)

Sjekk om grenser fra venstre og høyre i $x = 0$ gir samme verdi:

• Venstre: $\lim_{x \to 0^-} f(x) = 0^2 + 2 = 2$
• Høyre: $\lim_{x \to 0^+} f(x) = 2e^0 = 2$

Funksjonen $f$ er kontinuerlig i $x = 0$.

b)

Siden $g(0)=1$, og grenseverdiene i oppgave a) var 2, er $g$ ikke kontinuerlig i $x=0$.

DEL 2

Oppgave 1

a)

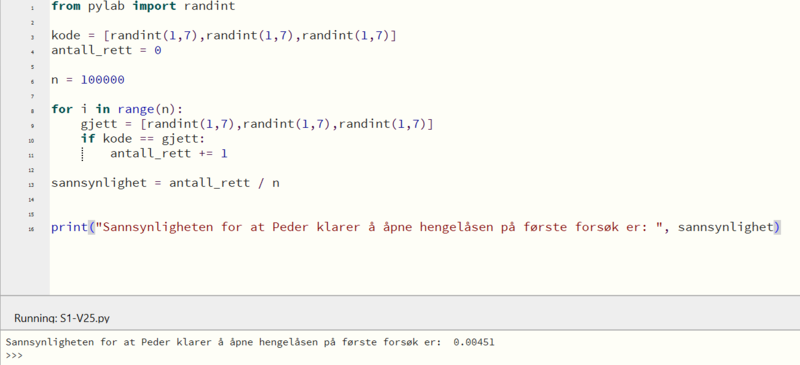
Med tallene 1,2,3,4,5,6 er det seks mulige tall på hver plass. Det gir $6^3=216$ mulige kombinasjoner.

Sannsynligheten for at Peder klarer å åpne hengelåsen på første forsøk er $\frac{1}{216}=0,00463$

b)

Oppgave 2

Vi bruker navnene $p(x)$, $q(x)$ og $r(x)$ som egendefinerte betegnelser for de tre delene av funksjonen, for å gjøre beregningene tydeligere der

$$ f(x) = \begin{cases} p(x), & x \leq -2 \\ q(x), & -2 < x < 1 \\ r(x), & x \geq 1 \end{cases} $$

$p(x)$ og $r(x)$ er gitt i oppgave, men siden $q$ er et ubestemt tredjegradspolynom kan vi bruke:

$$ q(x) = ax^3 + bx^2 + cx + d $$

• Linje 1-3: Definere $p$, $q$ og $r$ i CAS

Vi ønsker å finne uttrykket for $q(x)$ slik at $f$ er kontinuerlig i hele $\mathbb{R}$. Siden alle $p$, $q$ og $r$ er polynomer, er det bare nødvendig å sjekke i delingspunktene til $f$:

For $x = -2$:

• Kontinuerlig dersom $\lim_{x \to -2^-} f(x) = \lim_{x \to -2^+} f(x) \Rightarrow p(-2) = q(-2)$

• Linje 4: $p(-2) = q(-2)$
  • Obs! Selv om $q(-2)$ ikke er definert som funksjonsverdi (siden $q$ bare gjelder for $-2 < x < 1$), kan vi likevel bruke uttrykket $q(-2)$ i CAS for å representere høyre grenseverdi.*

For $x = 1$:

• Kontinuerlig dersom $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) \Rightarrow q(1) = r(1)$

• Linje 5: $q(1) = r(1)$

Linje 6-7 viser de to verdiene av den deriverte vi får i oppgaveteksten.

Linjer 4–7 utgjør et likningssystem.

• Linje 8: Løsning til likningssystemet:

$$ \begin{aligned} a &= -\frac{13}{27} \\ b &= \frac{7}{9} \\ c &= -\frac{1}{9} \\ d &= -\frac{113}{27} \end{aligned} $$

Det manglende uttrykket i midten av $f(x)$ er:

$$ q(x) = -\frac{13}{27}x^3 + \frac{7}{9}x^2 - \frac{1}{9}x - \frac{113}{27}, \quad \text{for } -2 < x < 1 $$