Løsning del 1 utrinn Vår 22: Forskjell mellom sideversjoner
| Linje 57: | Linje 57: | ||
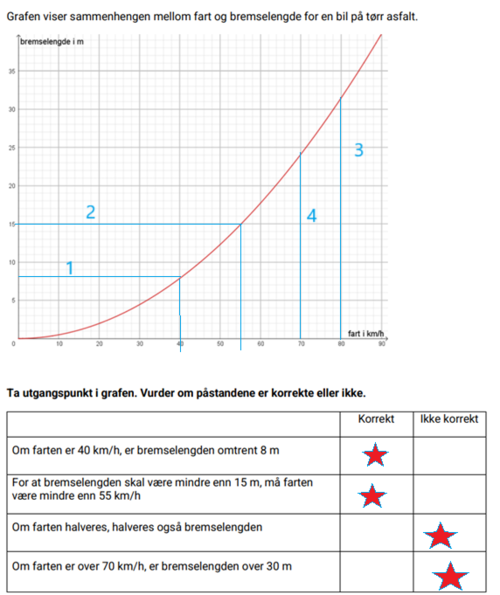
==Oppgave 5== | ==Oppgave 5== | ||
[[File:27032025-02.png|center|300px]] | |||
==Oppgave 6== | ==Oppgave 6== | ||
Sideversjonen fra 27. mar. 2025 kl. 07:40
Diskusjon av denne oppgaven på matteprat
Lenke til løsning del 2 av dette eksamenssettet
Videoløsning del 1 av Lektor Lainz
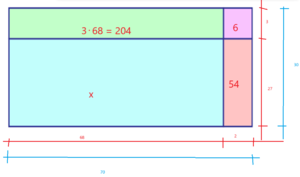
Oppgave 1
Prisen for en sjokolade: x
Prisen for en flaske vann: y
$ \left[ \begin{align*} 2x + y =40 \\ 4x + 3y = 98 \end{align*}\right] $
$ \left[ \begin{align*} y = 40 - 2x \\ 4x + 3(40 - 2x)= 98 \end{align*}\right]$
$4x + 120 -6x = 98$
$- 2x = -22$
$x = 11$
En sjokolade koster 11 kroner.
Oppgave 2
Oppgave 3
Vi tenker på en lengde som en positiv størrelse, det betyr at a er større enn null, altså $a > 0$.
Dette er en uheldig og uklar oppgave. Normalt tenker man at en lengde er lengre enn en bredde. Men, i denne oppgaven er bredden dobbelt så lang som lengden.
Lengden kan være et hvilket som helst positivt tall a. Da blir bredden dobbelt så lang, altså 2a.
Oppgave 4
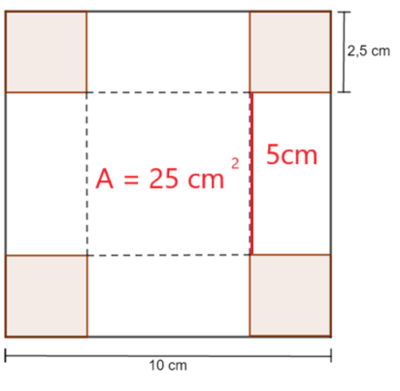
Vi ser at grunnflaten i boksen blir $5 cm \cdot 5 cm = 25 cm^2$. Høyden blir 2,5 cm.
$V = G \cdot h = 25 cm^2 \cdot 2,5 cm = 62,5 cm^3$.
Oppgave 5