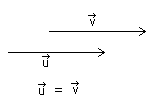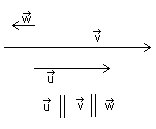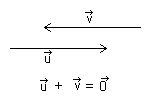Vektorregning

Introduksjon til vektorer

Fart er et eksempel på en vektor. Vi skiller vektorer fra skalare størrelser som er reelle tall (uten retning). Vektorer tegnes gjerne som piler (orientert linjestykke) i to og tredimensjonale systemer. Pilens orientering representerer retningen og lengden på pilen representerer størrelsen. Vektorer kan adderes og subtraheres. Vektorer kan også multipliseres med skalare størrelser (reelle tall).

Posisjon, fart, akselerasjon og kraft er eksempler på vektorer. Vektorer opptrer ofte mange sammen, for eksempel som strømning i en elv. Mange vektorer sammen kalles et vektorfelt. I fysikk regner man mye med vektorer.

En vektor er et geometrisk objekt som har både en størrelse og en retning. De avbildes som piler som peker i den aktuelle retningen og har en lengde lik vektorens størrelse.

En vektor er entydig bestemt ved å angi både dens størrelse og retning eller ved å angi dens komponenter.

Vektorkomponenter

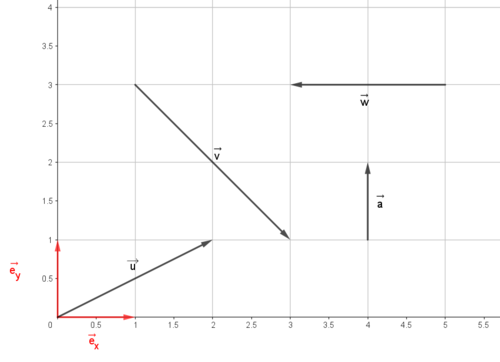
Vektorer i et koordinatsystem. $\vec{e_x}$ er en enhetsvektor. En vektor med lengde en, parallell x -aksen. På samme vis er $\vec{e_y} $ enhetsvektor i y-retning. Ved hjelp av disse to enhetsvektorene kan man uttrykke en hvilken som helst vektor i planet.

Komponentene til en vektor er gitt som vektorens lengde projisert på koordinataksene. For eksempel vil en vektor i planet som går fra (0,0) til (2,1) ha x-komponent 2 og y-komponent 1, som vi skriver som [2,1]. Det betyr egentlig $[2 \cdot \vec{e_x}, 1 \cdot \vec{e_y}]$. I figuren over er $\vec{u} = [2,1], \quad \vec{v}= [2, - 2], \quad \vec{w} = [-2, 0] , \quad \vec{a} = [0,1] $

Vektor mellom to punkter

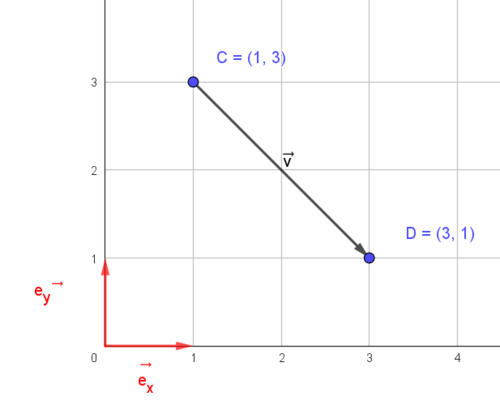
I to dimensjoner kan en vektor mellom to punkter uttrykkes som $ \vec{v}=[(x_2 - x_1),(y_2-y_1)]$ Vektoren i figuren over blir $\vec{v}=\vec{CD} = [(3-1), (1-3)] = [2,-2]$

I 3D: En vektor mellom punktene <math>A(a_1,a_2,a_3)</math> og <math>B(b_1,b_2,b_3)</math> kalles <math>\overrightarrow{AB}</math> (uttalt AB-vektor) og har komponentene <math>\overrightarrow{AB}=[b_1-a_1,b_2-a_2,b_3-a_3]</math>.

Vi har følgende regler for vektorer:

Like vektorer

To vektorer er like dersom vektorene har samme retning og samme lengde. En vektor er ikke "stedbundet", så u og v vektor er like så lenge retning og lengde er identiske.

Parallelle vektorer

2.To vektorer er parallelle dersom vektorene har samme retning eller motsatt retning.

Vektorsum

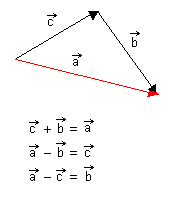
3.Dersom vi skal finne summen av vektoren c og vektoren b tegner vi først vektoren c. I endepunktet for c starter vi å tegne b. c + b vektor blir da vektoren som starter i begynnelsen av c og ender i enden av b, kalt a.

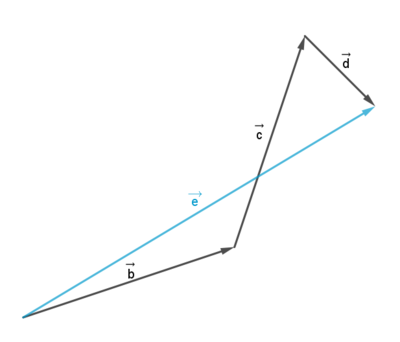
Figuren viser summen av vektorene b, c og d. Summen er vektor e. Vi ser at vi begynner med en vektor b, neste vektor starter der hvor b slutter. Samme så med vektor d. Husk at en vektor kan flyttes rundt i planet eller rommet uten at den forandres, så lenge vi ikke endrer lengde eller retning på den.

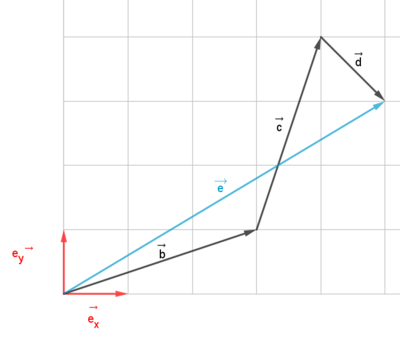
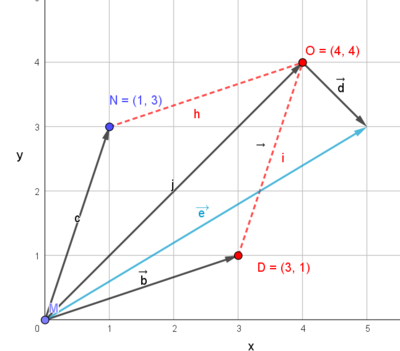
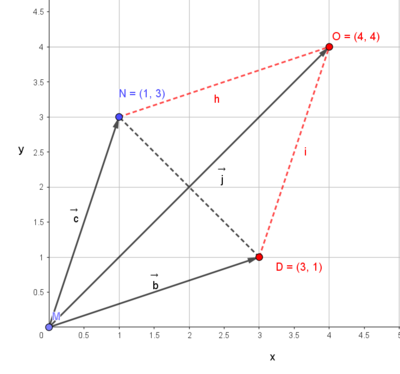
Her har man den samme vektorsummen, men nå i et koordinatsystem. Figuren til høyre viser "trapestankegangen". Her utspenner vektor b og c et trapes. Diagonalen i trapeset, j vektor er summen av b vektor pluss c vektor. Vi ser at $\vec{b} = [3,1] \quad \vec{c} = [1,3]$ og $\vec{d} = [1,-1]$

Trapesmetoden kan brukes når man ønsker å finne midtpunktet på en side i en trekant. Vi observerer at j vektor deler linjestykket DN i to like store deler. Vi observere også at skjæring skjer ved $\ \frac 12 \vec{j}$

Eksempel

Vi har en trekant ABC i et koordinatsystem, der A( 1,1), B( 6,2) og C(4,9). Finn midtpunktet på siden BC.

Løsning:

Vi lager først vektorene AB og AC:

$\overrightarrow{AB} = [6-1, 2-1] = [5, 1]$

$\overrightarrow{AC} = [4-1, 9-1] = [3, 8]$

Vi summerer AB og AC vektor, så deler vi på to (ganger med en halv), vi får da en vektor som tar oss til midtpunktet på BC. Vi kaller midtpunktet på BC for D:

$\overrightarrow{AD} = \frac 12 ( \overrightarrow{AB} + \overrightarrow{AC}) = \frac 12( [5,1] + [3,8] ) = \frac 12[8,9] = [4, \frac 92]$

Nullvektor

4.Nullvektor har lengde null og ingen rettning. Den er parallell med, og normalt på alle andre vektorer.

Lengden av en vektor

5.Lengen av n vektor skrives som

<math>| \vec n |</math>

I rommet

La <math>\vec{v}=[a,b,c]=a\vec{e_x}+b\vec{e_y}+c\vec{e_z}</math> være en vektor i rommet.

Da er lengden av vektoren definert som <math>|\vec{v}|=\sqrt{a^2+b^2+c^2}</math>

Enkelte lærebøker skriver lengden av en vektor slik: <math>||\vec{v}||</math>

Eksempel En vektor v har koordinatne : $\vec{v}= [1,2,3]$. Da blir lengden av vektoren $|\vec{v}| = \sqrt{1^2 + 2^2 +3^2} = \sqrt{1 + 4 + 9} = \sqrt{14}$

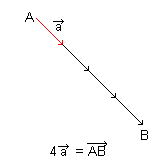
Vektor multiplisert med skalar

6.En vektor multiplisert med en skalar størrelse beholder retningen til den opprinnelige vektoren, men lengen øker med en faktor tilsvarende den skalare størrelsen.

Skalarprodukt

Et skalarprodukt er en regneoperasjon (multiplikasjon) mellom to vektorer. Skalarproduktet er et såkalt indreprodukt. Resultatet av regneoperasjonen er et reelt tall. Tallet bestemmes av lengden på vektorene og vinkelen mellom dem.

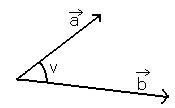
Vinkelen v mellom vektorene skal være element i intervallet [0°,180°]. Vi har vektorene <math>\vec{a}</math> og <math>\vec{b}</math>.

Skalarproduktet defineres som:

<math>\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}| cos(v)</math>

og leses "a vektor prikk b vektor er lik lengden av a vektor multiplisert lengden av b vektor multiplisert cosinus til vinkelen mellom dem".

Vektorene skrives av og til med fete typer og andre ganger med en liten pil over. Som man ser er det ikke konsekvens, man bør kjenne begge. På samme måte er det med lengden av en vektor, du vil støte på både |<math>\vec{v}</math>| og ||<math>\vec{v}</math>|| som notasjon, men begge betyr altså lengden av vektoren v.

Koordinatform

I planet

I et ortonormert koordinatsystem har vi følgende i planet:

Dersom vektoren <math>\vec{a} = [x_a,y_a]</math> og vektor <math>\vec{b} = [x_b,y_b]</math> har vi at

<math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b</math> Eksempelvis, dersom <math>\vec{a}</math> = [1,5] og <math>\vec{b}</math> = [-2,3] er skalarproduktet:

[1,5] · [-2,3] = -2 + 15 = 13

I rommet

Vektorene <math>\vec{a}= [x_a,y_a,z_a]</math> og <math>\vec{b}= [x_b,y_b,z_b]</math> gir skalarprodukt:

<math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b+z_az_b</math>

Praktisk bruk

Normale linjer

Skalarproduktet er egnet til å finne ut om to vektorer står vinkelrett på hverandre. Dersom vektorene a og b har lengder forskjellig fra null står vektoren normalt på hverandre hvis og bare hvis skalarproduktet er null.

a · b = 0

Arbeid

I fysikken brukes skalarproduktet i definisjonen av arbeid:

<math>W=\vec{F}\cdot\vec{s}</math>