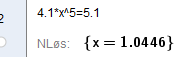2P 2021 høst LØSNING: Forskjell mellom sideversjoner
| Linje 161: | Linje 161: | ||
[[File:22122021-04.png]] | [[File:22122021-04.png]] | ||
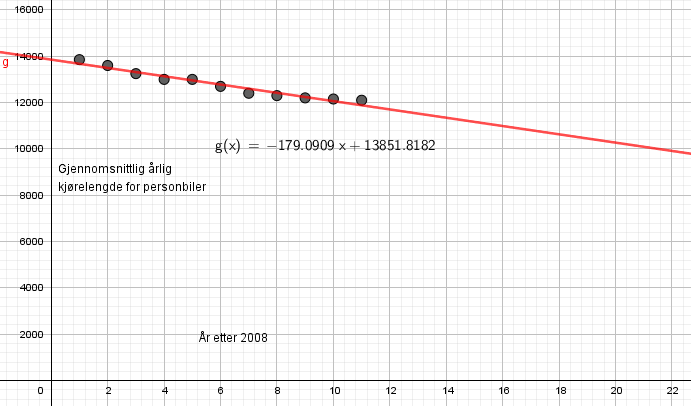
I følge modellen resuseres kjørelengden med ca 180 km per år (stigningstall). I | I følge modellen resuseres kjørelengden med ca 180 km per år (stigningstall). I 2007 var årlig kjørelengde i underkant av 14000 km (konstantledd). | ||
===b)=== | ===b)=== | ||
Få områder i samfunnet er så utsatt for politiske beslutninger som privatbilismen. Usikkerhet i alt fra subsidier av elbiler og forbud mot dieselbiler til utbygging av kollektive alternativer gjør det vanskelig å lage en modell egnet til å si noe om fremtiden. "Modellen" er etter vår mening kun gyldig i perioden 2008 til 2018. | |||
===c)=== | ===c)=== | ||
Sideversjonen fra 22. des. 2021 kl. 05:14
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
a)
00 444 55 77 9
Median er 4,5
Typetall er 4
Gjennomsnitt er 45/10 = 4,5
Variasjonsbredden er 9
b)
Den kumulative frekvensen for 5 dager med snø er 2+3+2= 7. Det betyr at i 7 av årene snør det fem dager eller sjeldnere i april.
Oppgave 2
a)
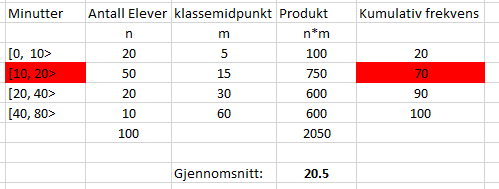
Gjennomsnittet i materialet er 20,5 minutter.
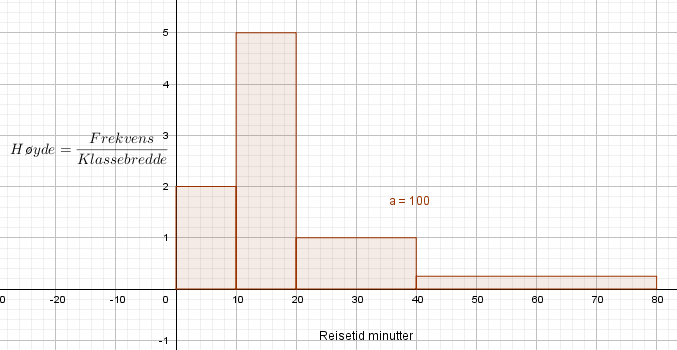
b)
Det ligger i intervallet 10-20. På kumulativ frekvens ser man at det intervallet inneholder verdiene fra nr 20 til 70, i stigende rekkefølge. Medianverdien er 50-51 og må følgelig befinne seg i intervallet.
c)
Oppgave 3
a)
$8^5= (2^3)^5=2^{3 \cdot 5} = 2^{15}$
b)
$3^{10}= 3^{2 \cdot 5} = 9^5> 8^5$
Oppgave 4
En fast prosent av et fast tall er det samme hele tiden. Men her endrer tallet eller grunnlaget seg, det vokser. Da blir også prosenten av grunnlaget større i tallverdi. Derfor tar Irene feil.
Gro har rett: vekstfaktoren finner man ut fra likningen $x^{10} = 1,14$ som gir x = 1,014 hvilket tilsvarer ca 1,4%. Så en økning på 1,4% per år gir en økning på 15% over 10 år. Husk at de 15% tar utgangspunkt i startverdien.
Andrea tar feil. Her er det ikke spørsmål om tallverdier, bare forhold mellom tall, som vist i avsnittet over. Dersom vi skulle sagt noe om dagens verdi på boligen i kroner, ville vi trengt mer informasjon.
Oppgave 5
a)
2000 :50 = 40 Altså smittes 40 nye hver dag, etter en lineær modell. $S(x) = 40x + 4000 $
b)
$S(x)=10000$
$40x + 4000 = 10000$
$40x =6000$
$x = 150$
Det tar 150 dager før antall smittede passerer 10 000.
Oppgave 6
a)
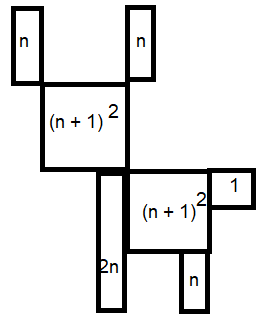
Vi prøver å uttrykke antall sirkler i forhold til figurens plassnummer:
Da kan man lage en generell sammenheng mellom figurnummer og antall sirkler.
$A(n)= 2(n+1)^2 +5n+1 = 2n^2+9n +2$
$A(5) = 2 \cdot 5^2+ 9 \cdot 5 + 2 = 50+45+2 = 97$
b)
Se a.
DEL TO
Oppgave 1
Butikk A i linje 1 og butikk B i linje 2.
Oppgave 2
På standardform: $1,5 \cdot 10^{10}$
Oppgave 3
a)
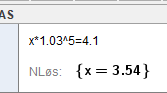
Det var vert 3,54 millioner kroner.
b)
Den årlige økningen er på 4,46%.
Oppgave 4
a)
b)
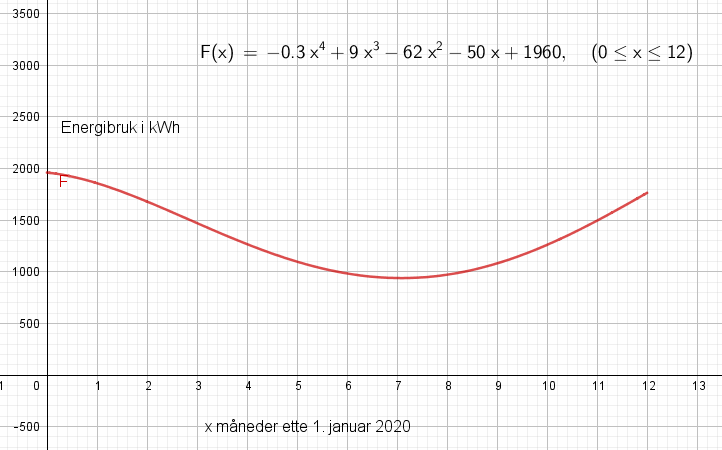
Fra figuren i a ser man at forbruket er over 1500 kWh i Januar, Februar og det meste av Mars, samt i Desember.
c)
Den momentane veksten forteller hvor stor endringen er den ene måneden.
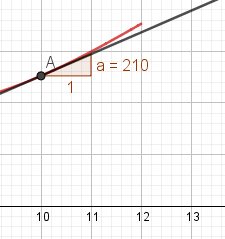 Veksten i forbruk i oktober var 210 kWh.
Veksten i forbruk i oktober var 210 kWh.
d)
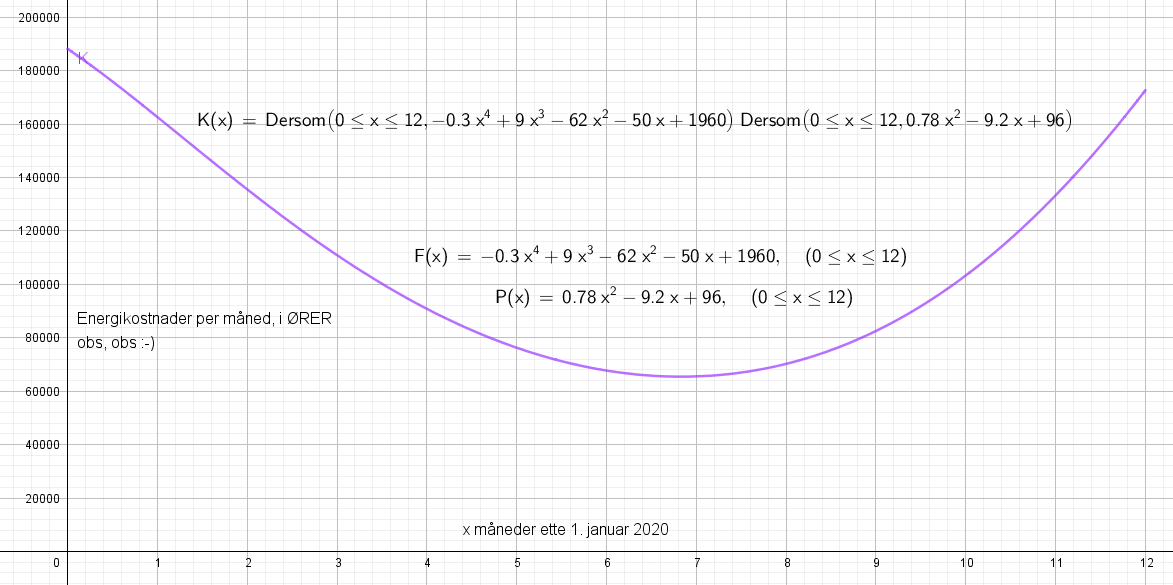
Dersom F er en funksjon for gjennomsnittlig forbruk i kWh og P gjennomsnittlig pris på kWh, må produktet FP være ett uttrykk for gjennomsnittlig energikostnad.
e)
Kostnadene var lavest i Juli.
Oppgave 5
a)
I følge modellen resuseres kjørelengden med ca 180 km per år (stigningstall). I 2007 var årlig kjørelengde i underkant av 14000 km (konstantledd).
b)
Få områder i samfunnet er så utsatt for politiske beslutninger som privatbilismen. Usikkerhet i alt fra subsidier av elbiler og forbud mot dieselbiler til utbygging av kollektive alternativer gjør det vanskelig å lage en modell egnet til å si noe om fremtiden. "Modellen" er etter vår mening kun gyldig i perioden 2008 til 2018.