2P 2021 høst LØSNING: Forskjell mellom sideversjoner
Fra Matematikk.net
| Linje 26: | Linje 26: | ||
Da kan man lage en generell sammenheng mellom figurnummer og antall sirkler. | Da kan man lage en generell sammenheng mellom figurnummer og antall sirkler. | ||
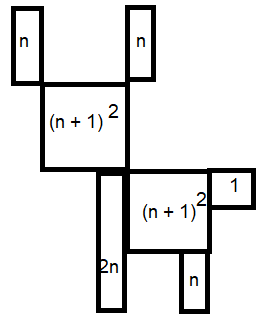
$A(n)= 2(n+1)^2 +5n+1 = 2n^2+9n +2$ | |||
$A(5) = 2 \cdot 5^2+ 9 \cdot 5 + 2 = 50+45+2 = 97$ | |||
===b)=== | ===b)=== | ||
==DEL TO== | ==DEL TO== | ||
Sideversjonen fra 20. des. 2021 kl. 03:23
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
Oppgave 6
a)
Vi prøver å uttrykke antall sirkler i forhold til figurens plassnummer:
Da kan man lage en generell sammenheng mellom figurnummer og antall sirkler.
$A(n)= 2(n+1)^2 +5n+1 = 2n^2+9n +2$
$A(5) = 2 \cdot 5^2+ 9 \cdot 5 + 2 = 50+45+2 = 97$