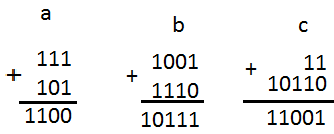Tallsystemer

Innledning

Det finnes mange tallsystemer. De har blitt utviklet gjennom historien og tilpasset tidens behov. Det systemet vi bruker mest er titallsystemet, men andre systemer er også synlige. Tid måles i sekunder og minutter, Det basere seg på 60, det Babylonske tallsystem.!http://per.matematikk.net/index.php?title=Babylonsk_matematikk Dersom man driver med data bør man kjenne to-, atte-, og 16 tallsystemet.

Romertall

I liket med andre kulturer benyttet romerne bokstaver for å symbolisere tall.

Titall	1	2	3	5	10	50	100	500	1000
Romertall	I	II	III	V	X	L	C	D	M

For å unngå mer enn tre like tegn ved siden av hverandre skrives for eksempel 4 som IV. Regelen er at når en bokstav med lavere verdi kommer foran en med større verdi, trekkes den laveste verdien fra den største (4 = 5 - 1). Systemet er lite praktisk å regne med.

Titallsystemet

Vi benytter til daglig et tallsystem vi kaller Titallsystemet. dekadisk system

Deka betyr ti og er det tallsystemet vi vanligvis bruker når vi regner. Vi har et system som er basert på ti siffer, disse er 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. Forskjellen på et tall og et siffer er at et tall kan bestå av et eller flere siffer. tallet 69 består for eksempel av to siffer, 6 og 9. I det dekadiske systemet er det enkelte tall som er spesielle. Vi kaller dem dekadiske enheter:

10 - ti

100 - hundre

1.000 - tusen

10.000 - titusen

100.000 - hundretusen

1.000.000 - en million

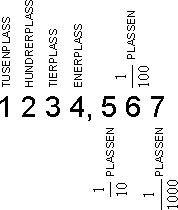
Titallsystemet benytter ti siffer, fra 0 til 9. Titallsystemet er et posisjonssystem. Det betyr at et siffer betydning, er avhengig av posisjon. Her er noen posisjoner:

Tallverdien er avhengig av sifferets verdi og posisjon.

Titallsystemet, gangetabell.

Syvtallsystemet

La oss bruke syv som grunntall i stede for ti. Syvtallsystemet er lite anvendt, utover mulig pedagogisk trening. For å skille de forskjellige tallene i de forskjellige tallsystemene fra hverandre bruker vi indekser. 100syv= ( 1·72 +0·71+0·70)ti= 49ti. På den annen side er 100ti=( 2·72 +0·71+2·70)ti= 202syv. Dette viser at forestillingen om "runde tall", er avhengig av tallsystem. Multiplikasjonstabellen ser slik ut:

Desimaltall EKS: (56,23)syv = ( 5·71 + 6·70+ 2·7-1 + 3·7-2)ti = ( 35 + 6 + 2/7 + 3/49)ti ≈ 41,347ti

Divisjon EKS:

Totallsystemet

Totallsystemet brukes mye i forbindelse med datamaskiner. Systemet består av sifrene 0 og 1, det medfører at tallene har en tendens til å bli lange og plasskrevende. Totall systemet er, i likhet med titallsystemet et posisjonssystem. Her er noen av tallene:

Totallsystem	Titallsystem
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
100000	32
1000000	64
10000000	128
100000000	256
1000000000	512
10000000000	1024

Bit og byte

Et siffer i den binære representasjonen av et tall, 1 eller 0. Tallet 1011 er representert ved fire bit. Det er en fundamental enhet i formaliseringen av informasjon. I datamaskiner er det slik at 1 representerer strøm på, signal går, og 0 representer strom av, signal går ikke. På den måten styrer datamaskinen alt du gjør, ved hjelp av matematikk.

Regneregler:

Fra totall til titall

Titallsystemet har "enerplass", "tierplass", "hundrerplass" osv. I totallsystemet har man fra venstre: "enerplass", "toerplass", "firerplass", "åtterplass" osv. Et tall i totallsystemet gjøres om til titall på denne måten:

<tex>110110 = 1 \cdot 2^5 + 1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 32 + 16 + 0 + 4 + 2 + 0 = 54 </tex>

Dette er potensregning med grunntall 2.

Regneregler

Addisjon

To tall skrives under hverandre. Dersim summen blir to settes en ener i posisjonen til venstre:

Multiplikasjon

La oss sjekke multiplikasjonen ved å gjøre om til titallsystemet. Dette er potensregning.

11101to= ( 1· 24 + 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20 )ti= (16 + 8 + 4 + 0 + 1)ti = 29ti.

10000001to = ( 1· 27 + 0 · 26 + 0 · 25 + 0 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20)ti = (128 + 1)ti=129ti.

111010011101to = ( 1 · 211 + 1 · 210 + 1 · 29 + 0 · 28 1· 27 + 0 · 26 + 0 · 25 + 1 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20)ti = (2048 + 1024 + 512 + 0 + 128 + 0 + 0 + 16 + 8 + 4 + 0 + 1)ti = 3741ti

I titallsystemet kan vi kontrollere: 29 · 129 = 3741

Vi har sett hvordan vi regner om fra totall- til titallsystemet. Når skal vi gå motsatt vei. Vi skal gjøre 324ti om til titallsystemet. Måten det gjøres på er at man dele på to (heltallsdivisjon) og beholder resten. Når vi deler på to kan resten bli en eller null. Vi bygger opp tallet i totallsystemet bakfra, som vist under.

324ti=?to

Som vi ser er 324ti=101000100to. Synes du totallsystemet blir for plasskrevende kan du jo sjekke ut det heksadesimale (16) tallsystemet.

Det Heksadesimale Tallsystem

Tallsystemet brukes mye innen it- faget. Her er noen av tallene:

EKS: A0Fseksten= (10 · 162 + 0 · 161 + 15 · 160) ti = (2560 + 0 + 15)ti = 2575ti