1P 2019 vår LØSNING

oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

DEL EN

a)

Bruker vekstfaktor.

$200 \cdot 1,15 = 230$

Det selges 230 biler i 2016.

b)

Antall biler gikk ned med 36. Nedgang i prosent:

$\frac{36}{240} \cdot 100 = 15$%

c)

Bruker vekstfaktor:

$x \cdot 0,8 = 200 \\ x= \frac{200}{0,8} \\ x = 250$

De solgte 250 biler i 2014.

Oppgave 2

$Reallønn = lønn \cdot \frac{100}{KPI} \\ KPI= \frac{lønn \cdot 100}{Reallønn}\\ KPI = \frac{550000 \cdot 100}{500000} \\KPI =110$

Oppgave 4

Når blandingsforholdet er 2:5 har vi totalt 7 deler som i dette tilfelle skal utgjøre 10,5 liter blanding. For å finne ut hvor stor en del er tar man 10,5 liter : 7 = 1,5 liter. Vi trenger altså 3 liter rengjøringsmiddel (to deler) og 7,5 liter vann.

a)

b)

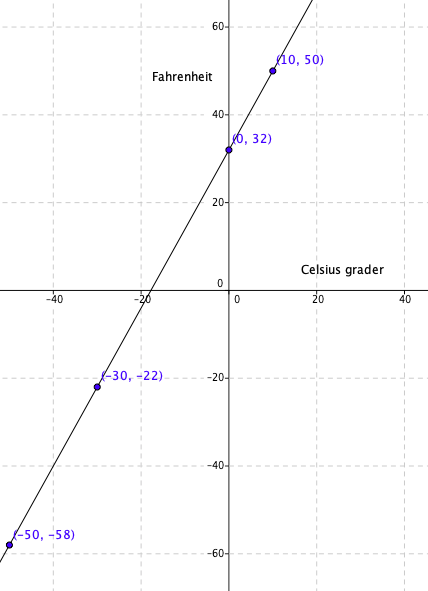
Størrelsene er ikke proporsjonale. Grafen til to proporsjonale størrelser er en rett linje gjennom origo.

c)

Fra figuren i a ser man at når det er $-40^{\circ}C$ er det også - 40 Fahrenheit. Begge gradestokkene vil da vise samme tallverdi.

d)

En rett linje er gitt som y= ax + b

I dette tilfelle er x = C og y = F, b = 32

Vi får da: F = aC + 32

For å finne stigningstallet, a, bruker vi de to siste punktene gitt i oppgaven ( 0, 32) og (10, 50). Man kan bruke hvile to punkter man vil men det lønner seg alltid å velge verdier som gir enklest mulig regning. Vi tar endring i y verdi delt på endring i x verdi:

$a = \frac{\Delta y}{\Delta x} = \frac{50 - 32}{10-0}= \frac{18}{10} = \frac 95$ som er stigningstallet. Sammenhengen blir da:

$F = \frac 95 C + 32$

e)

$ F(C) = \frac 95 C + 32 \\F(100) = \frac 95 \cdot 100 + 32 \\ F(100) = \frac{9 \cdot 100}{5} + 32 \\ F(100)= 9 \cdot 20 +32 = 212$

Altså er $100^{\circ} C = 212^{\circ}F$

Oppgave 6

a)

Hendelse M: I rute mandag - 80% Hendelse F: I rute fredag - 90%

Dersom begge henvendelsene skal inntreffe bruker vi multiplikasjonssetningen for å finne sannsynligheten:

P (M og F) = $P(M) \cdot P(F) = \frac{80}{100} \cdot \frac{90}{100} = \frac{7200}{10000}= \frac {72}{100} = 72$ %.

Det er 72% sannsynlig at toget er i rute begge dagene.

Oppgave 7

a)

Dersom åtte personer skal dele en kostnad på 18 000 kroner blir det 18000 : 8 = 2250

Hver person må betale kr. 2250,-

b)

Dette er omvendt proporsjonale størrelser, det blir billigere for den enkelte jo flere som er med, men prisen for den enkelte synker mest med de første som blir med.

$U(x)= \frac{18000}{x}$

c)

I den første grafen avtar det jevnt, med en fast verdi for en økning av x. Slik er det ikke i vårt tilfelle der det avtar mest i starten, altså er grafen til høyre en riktig beskrivelse av utviklingen.