S2 2018 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 4: | Linje 4: | ||
[https://github.com/matematikk/vgs_eksamener/blob/master/l%C3%B8sningsforslag/S2/S2_18V/S2_18V_lf.pdf Løsning laget av mattepratbruker Tommy O.] | [https://github.com/matematikk/vgs_eksamener/blob/master/l%C3%B8sningsforslag/S2/S2_18V/S2_18V_lf.pdf Løsning laget av mattepratbruker Tommy O.] | ||
=DEL 1= | |||
==Oppgave 1== | |||
===a)=== | |||
$f(x)=2x^3-4x+1 \\ f'(x) = 6x^2 - 4$ | |||
===b)=== | |||
$g(x)=\frac{x}{e^x} \\ g'(x)= \frac{1 \cdot e^x - x \cdot e^x}{(e^x)^2} = frac{e^x (1-x)}{(e^x)(e^x) = \frac{1-x}{e^x}$ | |||
===c)=== | |||
=DEL 2= | =DEL 2= | ||
Sideversjonen fra 23. mar. 2019 kl. 09:30
Diskusjon av denne oppgaven på matteprat
Løsning laget av mattepratbruker Tommy O.
DEL 1
Oppgave 1
a)
$f(x)=2x^3-4x+1 \\ f'(x) = 6x^2 - 4$
b)
$g(x)=\frac{x}{e^x} \\ g'(x)= \frac{1 \cdot e^x - x \cdot e^x}{(e^x)^2} = frac{e^x (1-x)}{(e^x)(e^x) = \frac{1-x}{e^x}$
c)
DEL 2
Oppgave 1
a)
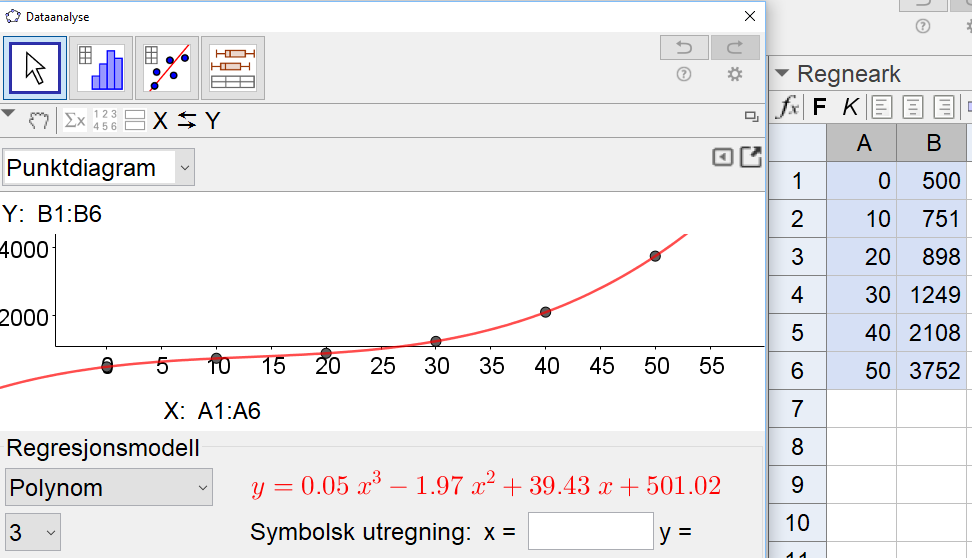
Bruker Geogebra til å utføre en regresjonsanalyse på punktene i tabellen. Velger polynomfunksjon av 3. grad som modell for kostnadene, h(x). Se skjermbildet under.
Jeg har funnet en modell for kostnaden, $h(x)=0,05x^3-1.97x^2+39,43x+501,02$
Inntekten er 80 kroner per enhet, og kan uttrykkes som $I(x)=80x$.
For å finne en modell for overskuddet, O(x), bruker jeg CAS i Geogebra, og regner ut O(x)=I(x)-h(x). Se skjermbildet under.
Jeg har dermed vist at funksjonen $O(x)=-0,05x^2+2,0x^2+41x-501$ (noe avrundet) er en god modell for det daglig overskuddet til bedriften ved produksjon av x enheter.