Løsning del 1 utrinn Vår 18

Vår 2018

a)

500g $\cdot$ 6 = 3000g = 3 kg

b)

3 km på 20 minutter. 20 minutter er $ \frac 13$ time: $v = \frac st = \frac{3km}{\frac13 time} = 3 km \cdot \frac 31 time= 9 $ km /t

Gjennomsnittsfarten er 9 km/h.

a)

$2^3 - 2 = 8-2 =6$

b)

$\frac{2^2\cdot 2^4}{2+2} = \frac{4 \cdot 16}{4} = 16$

Oppgave 3

$ 7,5 \quad \sqrt{64}=8 \quad 3\pi > 9,4 \quad \frac{36}{4} = 9$

Den laveste verdien er 7,5

a)

$1-( \frac 15 + \frac 14) = 1- (\frac{4}{20} + \frac{5}{20}) = 1- \frac{9}{20} = \frac{11}{20} = \frac{55}{100}$

Altså 55%

b)

$40 \cdot \frac 15 = 8 $, altså 8 strategispill.

Oppgave 5

For fire personer finnes det 4! mulige rekkefølger:

$4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24$

a)

Sannsynligheten for gul blir antall gunstige delt på antall mulige, altså: P ( gul) = $ \frac{23}{102}$.

b)

Sannsynligheten for ikke å trekke sort kan skrives slik: $P( \overline{sort})$

Tar de Nonstoppene som ikke er sorte og deler på antall mulige:

$P( \overline{sort}) = \frac{82}{102} = \frac{41}{51}$

Oppgave 7

$7500 000 000= 7 ,5\cdot 10^9 $

Oppgave 8

$48,50 : 13,90 = \\485 : 139 \approx 3,5$

Hun kjøper ca 3,5 hg smågodt.

Oppgave 9

$4y = 180^{\circ} \\ y= 45^{\circ}$

Vinkel y er 45 grader.

a)

3(a+2) -2a = 3a+ 6 -2a = a + 6

b)

$ \frac{a^2+a}{2a+2} = \frac{a(a+1)}{2(a+1)} = \frac a2$

a)

$6x+3 = 17 - x \\ 7x = 14 \\ x = 2$

b)

$x - \frac{x}{3} = \frac{x+1}{2} \quad | \cdot 6 \\ 6x -2x = 3(x+1) \\ 4x = 3x+3 \\ x = 3 $

Oppgave 12

Espresso og melk i forholdet 1: 3, altså fire deler til sammen. Dersom blandingen er 6dl utgjør en del $\frac 64$ = 1,5 dl. Tre deler blir da 4,5 dl.

a)

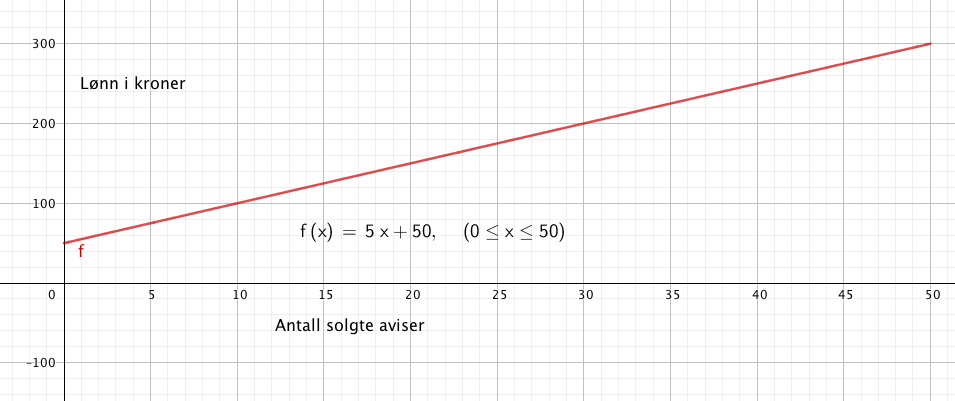
Fastlønn på kr. 50 og 5 kroner per solgt avis gir en lønn y på:

y = 5x + 50 , der x er antall solgte aviser.

b)

Grafen viser lønn som funksjon av antall solgte aviser i intervallet null til femti aviser.

Oppgave 14

Vinkelsummen i en trekant er 180 grader. En femkant kan deles i tre trekanter så vinkelsummen blir tre ganger så stor, altså $540^{ \circ} $.

Oppgave 15

Sirkel A, radius x: $O_A = 2 \pi r = 2 \pi x$

Sirkel B, radius 2x: $O_B = 2 \pi r = 2 \pi (2x) = 4 \pi x$

Omkretsen av sirkel B er dobbelt så lang som omkretsen av sirkel A.

Oppgave 16

Pris ball : x

Pris bukse: y

<math> \left[ \begin{align*}2x+y=2100 \\ 3x + y = 3000 \end{align*}\right] </math>

Ganger den første likningen med minus en og legger likningene sammen.

<math> \left[ \begin{align*}-2x-y=-2100 \\ 3x + y = 3000 \end{align*}\right] </math>

x= 900

Setter inn i likning en og finner at y= 300.

Buksa koster 300 kroner og ballen koster 900 kroner.

a)

Tre til fire timer: 25% $= \frac{25}{100} = \frac 14$

b)

30% av 63600:

$\frac{30 \cdot 63600}{100} =30 \cdot 636 = 19080$

19080 personer bruker mere enn fire timer i snitt foran en skjerm.

a)

Det horisontale kateter har lengden 10m - 4m - 2m = 4m, og det vertikale har lengden 3m.

Pytagoras: $x^2 = (4m)^2 + (3m)^2 = 25m^2 \\ x = \sqrt{25m^2} = 5m$

Lengden av x er fem meter.

b)

Omkrets av sammensatt figur, begynner øverst i trekanten og går mot klokka:

O = 5,0 m + 10,0 m +5,0 m + 4,0 m + 3,0 m + 2,0 m + 5,0 m = 34,0 m

c)

Deler opp den sammensatte figuren i en trekant og to rektangler:

$A = \frac{3m \cdot 4m}{2} + 10m \cdot 2 m + 4m \cdot 3 m \\ A = 6m^2 + 20m^2 + 12m^2 \\ A = 38m^2$

Oppgave 19

Sylinder: $V_{sylinder} = \pi r^2h = 2 \pi r^3$

Kule: $V_{kule} = \frac 43 \pi r^3$

Kjegle: $V_{kjegle} = \frac{\pi r^2h}{3} = \frac 23 \pi r^3$

$V_{kule} + V_{kjegle} = \frac 43 \pi r^3 + \frac 23 \pi r^3 = \frac 63 \pi r^3 =2 \pi r^3= V_{sylinder}$