1T 2018 vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning laget av LektorNilsen

DEL EN

Oppgave 1

<math> \left[ \begin{align*}5x +2y =4 \\ 3x + 4y = -6 \end{align*}\right] </math>

Ganger første likning med -2 for å bruke addisjon, slik at y forsvinner.

<math> \left[ \begin{align*}- 10x - 4y = -8\\ 3x + 4y = -6 \end{align*}\right] </math>

Legger likningen sammen og får

$-7x = -14 \\ x=2$

Setter x = 2 inn i første likning og får at y er:

$5x+2y =4 \\ 10 + 2y = 4 \\ 2y = -6 \\ y = -3$

Løsning: $x= 2 \wedge y= -3$

Oppgave 2

$3 \cdot 10^x = 3000 \\ 10^x = 1000 \\ x lg 10 = lg 1000 \\ x \cdot 1 = lg 1000 \\ x = 3$

Oppgave 3

$ \frac{(0,5 \cdot 10^6)^2}{0,2 \cdot 10^{-4} + 3 \cdot 10^{-5}} = \frac{0,25 \cdot 10^{12}}{2 \cdot 10^{-5} + 3 \cdot 10^{-5}} = \frac{25 \cdot 10^{10}}{5 \cdot 10^{-5}} = 5 \cdot 10^{15} $

Oppgave 4

$\sqrt{15 }\cdot \sqrt5 - \sqrt{48} = \sqrt {3 \cdot 5 \cdot 5} -\sqrt{4 \cdot 4 \cdot 3 } = 5 \sqrt3 - 4 \sqrt 3 =\sqrt 3$

Oppgave 5

$lg1000 \cdot lg \sqrt[3]{10} \cdot lg \sqrt[5]{10^2} \cdot lg 0,00001 \\= lg10^3 \cdot lg10^{\frac{1}{3}} \cdot lg10^{\frac{2}{5}} \cdot lg10^{-5} \\ = 3 \cdot \frac{1}{3} \cdot \frac{2}{5} \cdot (-5) = -2$

a)

$x (x+2) (x-4) = x (x^2-4x+2x-8) = x ( x^2 - 2x - 8) = x^3 -2x^2-8x$

b)

$x^3 -2x^2-8x = 0 \\ x (x+2) (x-4) = 0 \\ x=-2 \wedge x=0 \wedge x=4$

Oppgave 7

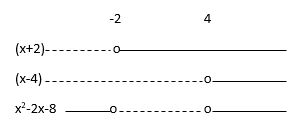
$ x^2-2x-8=0 \\ (x+2)(x-4)=0 \\ x=-2 \wedge x=4 $

$ x^2-2x-8 \geq 0 $ for $x<-2$ og $x>4$

Oppgave 8

Bruker abc-formelen $x = \frac{-b \sqrt{b^2- 4ac}}{2a}$ for å finne funksjonens nullpunkter, a=1, b=k, c=4.

$ x^2 +kx + 4 = 0 \\ x = \frac{-k \sqrt{k^2- 4 \cdot 1 \cdot 4}}{2 \cdot 1} \\ x = \frac{-k \sqrt{k^2- 16}}{2} $

Dersom likningen er uløselig, har grafen til f ingen skjæringspunkter med x-aksen (dvs. ingen nullpunkter). Dette skjer dersom verdien under kvadratroten er negativ, siden kvadratroten av et negativt tall ikke gir noen reelle løsninger.

Dersom verdien under kvadratroten er 0, får likningen bare én løsning, og grafen til f bare ett skjæringspunkt med x-aksen (dvs. ett nullpunkt).

Dersom verdien under kvadratroten er positiv, får likningen to løsninger, og grafen til f to skjæringspunkter med x-aksen (dvs. to nullpunkt).

Vi løser likningen $k^2-16 = 0$ for å finne hvilke verdier av k oppfyller de ulike mulighetene.

$k^2=16 \\ k= \pm \sqrt{16} \\ k=-4 \wedge k=4$

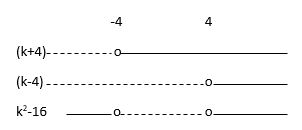
Vi ser at grafen til f har

$\bullet$ ingen skjæringspunkter med x-aksen for $-4<k<4$

$\bullet$ ett skjæringspunkt med x-aksen for $k=-4$ og $k=4$

$\bullet$ to skjæringspunkter med x-aksen for $k<-4$ og $k>4$