1T 2018 vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning laget av LektorNilsen

DEL EN

Oppgave 1

<math> \left[ \begin{align*}5x +2y =4 \\ 3x + 4y = -6 \end{align*}\right] </math>

Ganger første likning med -2 for å bruke addisjon, slik at y forsvinner.

<math> \left[ \begin{align*}- 10x - 4y = -8\\ 3x + 4y = -6 \end{align*}\right] </math>

Legger likningen sammen og får

$-7x = -14 \\ x=2$

Setter x = 2 inn i første likning og får at y er:

$5x+2y =4 \\ 10 + 2y = 4 \\ 2y = -6 \\ y = -3$

Løsning: $x= 2 \wedge y= -3$

Oppgave 2

$3 \cdot 10^x = 3000 \\ 10^x = 1000 \\ x lg 10 = lg 1000 \\ x \cdot 1 = lg 1000 \\ x = 3$

Oppgave 3

$ \frac{(0,5 \cdot 10^6)^2}{0,2 \cdot 10^{-4} + 3 \cdot 10^{-5}} = \frac{0,25 \cdot 10^{12}}{2 \cdot 10^{-5} + 3 \cdot 10^{-5}} = \frac{25 \cdot 10^{10}}{5 \cdot 10^{-5}} = 5 \cdot 10^{15} $

Oppgave 4

$\sqrt{15 }\cdot \sqrt5 - \sqrt{48} = \sqrt {3 \cdot 5 \cdot 5} -\sqrt{4 \cdot 4 \cdot 3 } = 5 \sqrt3 - 4 \sqrt 3 =\sqrt 3$

Oppgave 5

$lg1000 \cdot lg \sqrt[3]{10} \cdot lg \sqrt[5]{10^2} \cdot lg 0,00001 \\= lg10^3 \cdot lg10^{\frac{1}{3}} \cdot lg10^{\frac{2}{5}} \cdot lg10^{-5} \\ = 3 \cdot \frac{1}{3} \cdot \frac{2}{5} \cdot (-5) = -2$

a)

$x (x+2) (x-4) = x (x^2-4x+2x-8) = x ( x^2 - 2x - 8) = x^3 -2x^2-8x$

b)

$x^3 -2x^2-8x = 0 \\ x (x+2) (x-4) = 0 \\ x=-2 \wedge x=0 \wedge x=4$

Oppgave 7

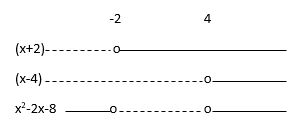
$ x^2-2x-8=0 \\ (x+2)(x-4)=0 \\ x=-2 \wedge x=4 $

$ x^2-2x-8 \geq 0 $ for $x<-2$ og $x>4$

Oppgave 8

Bruker abc-formelen, a=1, b=k, c=4.

$ x^2 +kx + 4 = 0 \\ x = \frac{-k \sqrt{k^2- 4 \cdot 1 \cdot 4}}{2 \cdot 1} $