Bevis -derivasjon sinus

f(x) = sin(x)

$ f' (x) = lim_\Delta x \rightarrow 0 = \frac {sin(x + \Delta x)- sin(x)}{\Delta x}$

Grenseverdiene $lim \frac{sin(x)}{x} $ og $lim \frac{cos(x)-1}{x}$

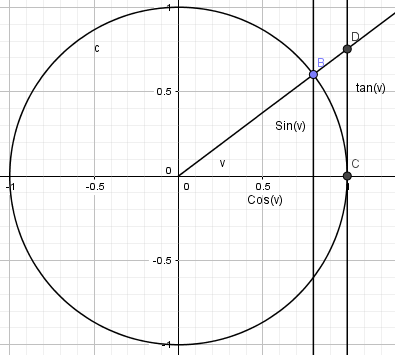
Tangens til v er lik lengden av linjestykke CD. De to trekantene er formlike og sirkelen har radius 1: $\frac{sin(v)}{cos(v)} = \frac{tan(v)}{1}$. som gir oss en definisjon for tangens som vi kjenner fra før.

Buelengden BC har har lengden v radianer, siden radius er 1. Buelengden BC er lengre enn Sin(v), men kortere enn Tan(v) (observasjon). Vi får da:

$ sin(v)< v < tan(v) \\ 1 < \frac{v}{sin(v)} < \frac{1}{cos(v)} \\ 1> \frac{sin (v)}{v}> cos(v) $

Når v går mot null går cos(v) mot 1. $\frac{sin(v)}{v}$ ligger mellom to størrelser som begge går mot en når x går mot null. Derfor er:

$\lim_{x \to \ 0} \frac{sin(v)}{v} =1$