Integralkurver: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| Linje 10: | Linje 10: | ||
Ser vi på differensialligningen <tex>f^,(x)=f(x)</tex> er løsningen på formen <tex>f(x)=ce^{x}</tex>. Integralkurvene kan vi skissere i et koordinatsystem ved f.eks. å tegne kurvene <tex>y=e^x</tex> , <tex>y=1.5e^x</tex>, <tex>y=2e^x</tex>, <tex>y=3e^x</tex> osv. | Ser vi på differensialligningen <tex>f^,(x)=f(x)</tex> er løsningen på formen <tex>f(x)=ce^{x}</tex>. Integralkurvene kan vi skissere i et koordinatsystem ved f.eks. å tegne kurvene <tex>y=e^x</tex> , <tex>y=1.5e^x</tex>, <tex>y=2e^x</tex>, <tex>y=3e^x</tex> osv. Legg merke til at de ulike integralkurvene aldri krysser hverandre. | ||
Sideversjonen fra 9. feb. 2010 kl. 12:00
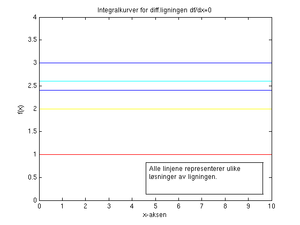
For å illustrere hva som menes med integralkurver går vi tilbake til den enkle differensialligningen <tex>f^,(x)=0</tex> med løsning <tex>f(x)=c</tex>. Her ser vi at alle konstante funksjoner er løsninger siden vi ikke har spesifisert verdien av konstanten <tex>c</tex>. Med integralkurver menes simpelthen løsningskurver for forskjellige verdier av <tex>c</tex>. Mengden av integralkurver for denne diff.ligningen blir mengden av alle horisontale linjer.
Eksempler
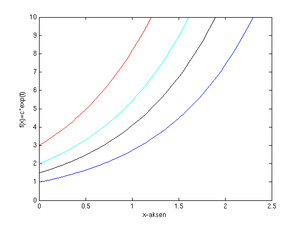
Ser vi på differensialligningen <tex>f^,(x)=f(x)</tex> er løsningen på formen <tex>f(x)=ce^{x}</tex>. Integralkurvene kan vi skissere i et koordinatsystem ved f.eks. å tegne kurvene <tex>y=e^x</tex> , <tex>y=1.5e^x</tex>, <tex>y=2e^x</tex>, <tex>y=3e^x</tex> osv. Legg merke til at de ulike integralkurvene aldri krysser hverandre.