Løsning del 2 utrinn Vår 15 eksempeloppgave: Forskjell mellom sideversjoner
| Linje 9: | Linje 9: | ||
==Oppgave 1 == | ==Oppgave 1 == | ||
===a)=== | |||
===b)=== | |||
==Oppgave 2== | ==Oppgave 2== | ||
Sideversjonen fra 15. des. 2015 kl. 07:36
- Oppgaven Del 1 som pdf
- Løsning del 1
- Oppgaven Del 2 som pdf
- Løsning på oppgaven som pdf
- Løsning på oppgaven på doc-format
- Løsning på oppgave 4, 7, 9 og 10 løst med ggb cas og grafikk som pdf
- Løsning av alle oppgaver som videoer
Oppgave 1
a)
b)
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
Oppgave 6
Oppgave 7
Løsning på denne oppgaven som video laget av Mette Bendiksen
Oppgave 8
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.
Oppgave 9
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
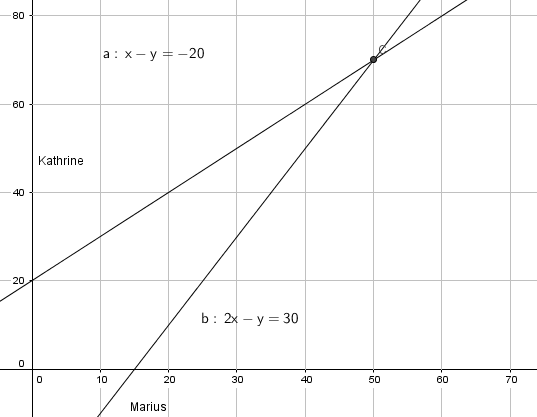
Marius: "Gi meg 10 klinkekuler, så har vi like mange" gir oss: x +10 = y - 10 som er lik x - y = -20.
Kathrine: "Hvis du i stedet gir meg 10 klinkekuler, så vil jeg ha dobblt så mange som deg" gir oss:
$2(x - 10) = y+ 10 \\ x - 20 = y + 10 \\ 2x -y = 30$
b)
Vi ser at Marius har 50 kuler og Kathrine har 70.
c)
\begin{bmatrix} x-y = -20 \\ 2x-y=30 \end{bmatrix} \begin{bmatrix} -x+y=20 \\ 2x-y = 30 \end{bmatrix} \begin{bmatrix} 2x-x=20+30 \end{bmatrix}
\begin{bmatrix} x = 50 \end{bmatrix}
Innsatt for x = 50 gir det 50 - y = -20, dvs y = 70
$x=50 \wedge y=70$
Marius har 50 kuler og Kathrine har 70.
Oppgave 10
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Område 1: $20m \cdot 50m = 1000m^2$
Område 2: $60m \cdot 10m = 600m^2$
b)
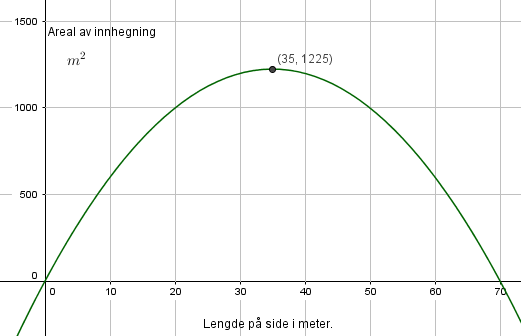
Dersom to av sidene er x er lengden som er igjen til de to andre sidene lik 140- 2x. Når man deler på 2 finner man at en av disse sidene må være 70-x.
$A(x)= x(70 - x) = -x^2 +70x$
x kan ligge mellom 0 og 70 meter. $x \in [0, 70]$