S2 2015 høst LØSNING: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: ==DEL 1== ==Oppgave 1== ==a)== $f(x)=x^3+2x \\ f'(x)=3x^2+2$ ==b)== $g(x)=3e^{2x-1} \\ g'(x)=3e^{2x-1} \cdot (2x-1)'=6e^{2x-1}$ ==c)== $h(x)=x^2 \cdot e^x \\ h'(x)=2xe^x+x^2e^x=xe^x(2+x)... |
|||
| Linje 9: | Linje 9: | ||
==Oppgave 2== | ==Oppgave 2== | ||
==a)== | ==a)== | ||
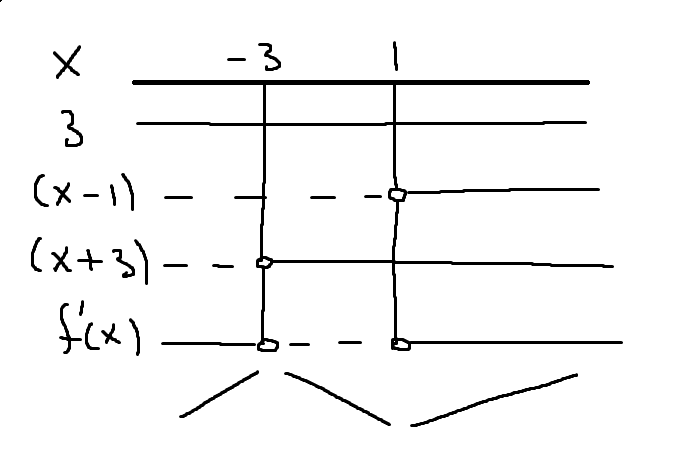
$f(x)=x^3+3x^2-9x \\ f'(x)=3x^2+6x-9=3(x^2+2x-3)=3(x-1)(x+3)$ | |||
Alternativt kan $f'(x)$ faktoriseres med ABC-formelen | |||
[[File:s2.png]] | |||
Toppunkt: $T=(-3,f(-3))=(-3,-27+27+27)=(-3,27)$ | |||
Bunnpunkt: $B=(1,f(1))=(1,1+3-9)=(1,-5)$ | |||
==b)== | ==b)== | ||
Sideversjonen fra 7. des. 2015 kl. 19:21
DEL 1
Oppgave 1
a)
$f(x)=x^3+2x \\ f'(x)=3x^2+2$
b)
$g(x)=3e^{2x-1} \\ g'(x)=3e^{2x-1} \cdot (2x-1)'=6e^{2x-1}$
c)
$h(x)=x^2 \cdot e^x \\ h'(x)=2xe^x+x^2e^x=xe^x(2+x)$
Oppgave 2
a)
$f(x)=x^3+3x^2-9x \\ f'(x)=3x^2+6x-9=3(x^2+2x-3)=3(x-1)(x+3)$
Alternativt kan $f'(x)$ faktoriseres med ABC-formelen
Toppunkt: $T=(-3,f(-3))=(-3,-27+27+27)=(-3,27)$
Bunnpunkt: $B=(1,f(1))=(1,1+3-9)=(1,-5)$