S1 2015 vår LØSNING: Forskjell mellom sideversjoner
Fra Matematikk.net
| Linje 111: | Linje 111: | ||
===a)=== | ===a)=== | ||
[[File:s1-v2015-3ab.png]] | [[File:s1-v2015-3ab.png]] | ||
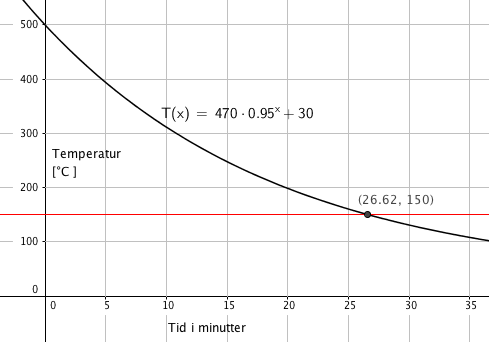
Metallet er 500 grader celsius når det blir tatt ut av ovnen, fra figur. Har også at $T(0)= 470+30 = 500$ | |||
===b)=== | ===b)=== | ||
Sideversjonen fra 28. sep. 2015 kl. 06:04
Diskusjon av denne oppgaven på matteprat
Løsning laget av matteprat-bruker LektorH
DEL EN
Oppgave 1
a)
b)
Oppgave 2
a)
b)
Oppgave 3
a)
$(a+1)^2 - 2(a-1)(a+1) + (a-1)^2 = \\ a^2+2a+1 -2(a^2-1) +a^2 -2a+1=\\ a^2 +2a+1-2a^2+2+a^2-2a+1=\\ 4$
b)
$\frac{(2a^2)^{-1}(3b)^2}{(3a^2b^{-1})^2} \\ \frac{9b^2b^2}{18a^6}= \\ \frac{b^4}{2a^6}$
Oppgave 4
a)
$f(x)= x^3 -6x^2+9x-4 \quad D_f = \R \\ f´(x) = 3x^2-12x+9$
b)
c)
d)
Oppgave 5
a)
b)
Oppgave 6
a)
b)
Oppgave 7
a)
b)
c)
Oppgave 8
a)
b)
Oppgave 9
DEL TO
Oppgave 1
a)
b)
c)
Oppgave 2
a)
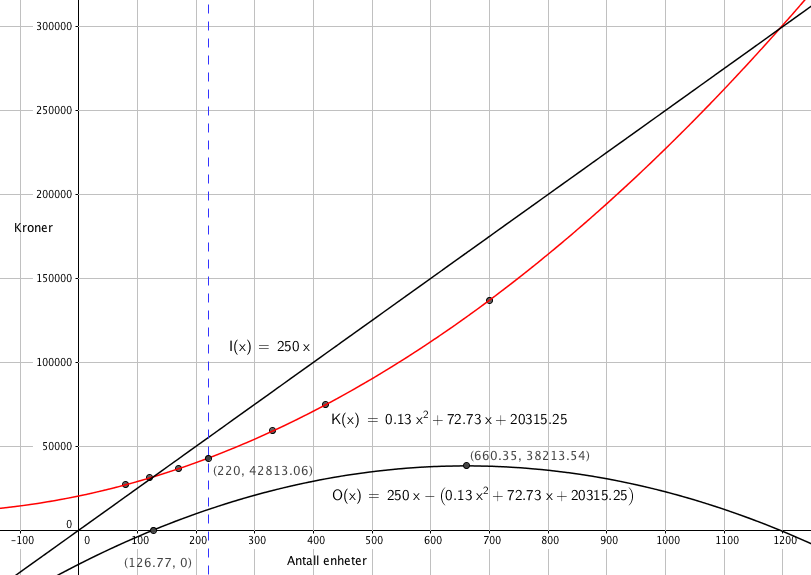
En god modell er $K(x)=0,13x^2+72,73x+20315$
Kostnadene ved å produsere 220 enheter er 48.813 kroner.
b)
Fra figur i a:
For å få overskudd må bedriften produsere og selge 127 eneheter.
c)
Fra figur i a:
Størst overskudd ved 660 enheter, da er overskuddet 38.213,50 kr.
Oppgave 3
a)
Metallet er 500 grader celsius når det blir tatt ut av ovnen, fra figur. Har også at $T(0)= 470+30 = 500$