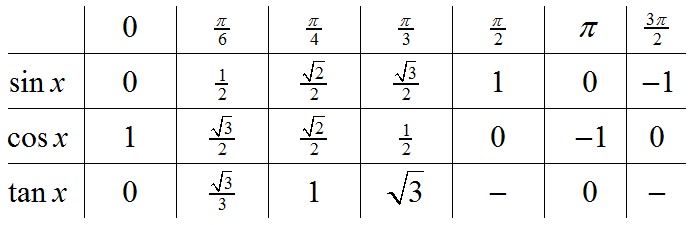Trigonometri R2: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| Linje 40: | Linje 40: | ||
Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <tex>\tan\,x</tex> går mot <tex>\pm\infty</tex>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <tex>\tan\,x</tex> når <tex>x=\frac{\pi}{2}</tex> eller <tex>x=\frac{3\pi}{2}</tex>. | Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <tex>\tan\,x</tex> går mot <tex>\pm\infty</tex>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <tex>\tan\,x</tex> når <tex>x=\frac{\pi}{2}</tex> eller <tex>x=\frac{3\pi}{2}</tex>. | ||
===Noen viktige verdier av sin x, cos x og tan x=== | |||
Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger. | |||
[[Bilde:Trigverdier.png]] | |||
==Sumformelen for sin x og cos x== | ==Sumformelen for sin x og cos x== | ||
Sideversjonen fra 18. jan. 2010 kl. 21:39
Absolutt vinkelmål
Radianer (også kalt absolutt vinkelmål) er definert ved at <tex>360^\circ = 2\pi\</tex> radianer.
Trigonometeriske funksjoner
De tre sentrale trigonometriske funksjonene er sinus, cosinus og tangens, som er et produkt av sinus og cosinus. Sinus er den viktigste trigonometriske funksjonen, siden alle de andre trigonometriske funksjonene kan utledes fra denne.
Definisjon av sin x og cos x
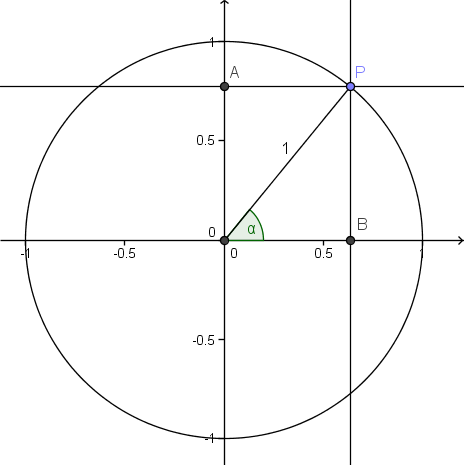
Ta utgangspunkt i figuren under:
Når vi konstruerer en enhetssirkel og en radius med vinkel <tex>\alpha</tex> på x-aksen slik figuren viser, vil radien skjære sirkelperiferien i punktet <tex>P</tex>. Hvis trekker normalene fra <tex>P</tex> på koordinataksene, vil de skjære disse i punktene <tex>A</tex> og <tex>B</tex> slik figuren viser. Da vil y-verdien til punktet <tex>A</tex> være lik <tex>\sin\,\alpha</tex> og x-verdien til punktet <tex>B</tex> være lik <tex>\cos\,\alpha</tex>
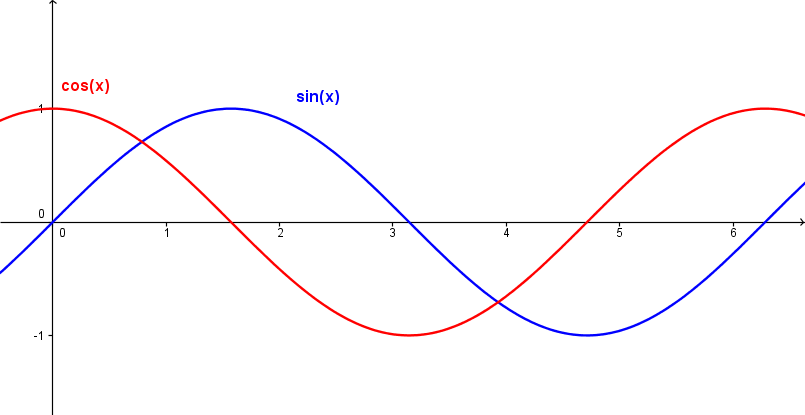
Når vi plotter sinus- og cosinuskurvene ser de slik ut:
Sinus- og cosinuskurvene har begge perioder på <tex>2\pi</tex> radianer.
Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet <tex>\frac{\pi}{2}</tex> radianer i minusretningen. Altså gjelder det at <tex>sin(x+\frac{\pi}{2})=\cos\,x</tex>
Definisjon av tan(x)
Tangensfunksjonen er definert slik at
<tex>\tan\,x=\frac{\sin\,x}{\cos\,x}</tex>
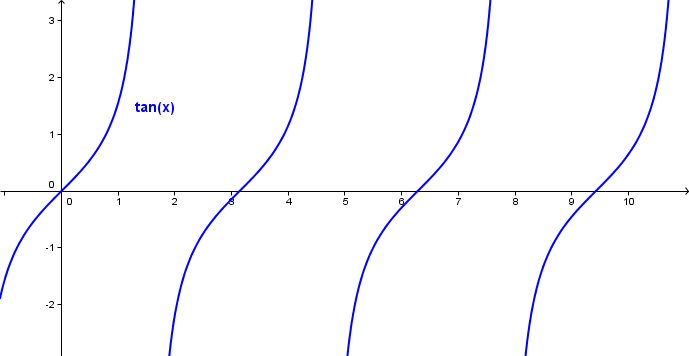
Når vi plotter tangenskurven, ser den slik ut:
Tangenskurven har en periode på <tex>\pi</tex> radianer.
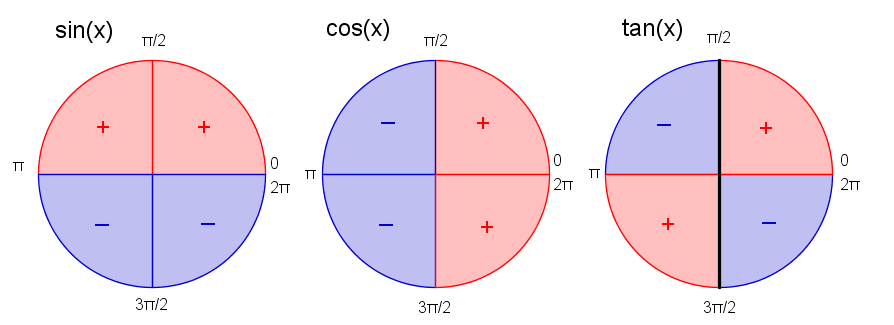
Fortegn av trigonometriske funksjoner
Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der <tex>\tan\,x</tex> går mot <tex>\pm\infty</tex>. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til <tex>\tan\,x</tex> når <tex>x=\frac{\pi}{2}</tex> eller <tex>x=\frac{3\pi}{2}</tex>.
Noen viktige verdier av sin x, cos x og tan x
Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger.