1T 2014 høst LØSNING

• Diskusjon av denne oppgaven

• Løsning av del 1

• Matteprat spørsmål om oppgave 6 del 2

Oppgave 1

$25000000000 \cdot 0,0005 = 2,5 \cdot 10^{10} \cdot 5 \cdot 10^{-4} = 12,5 \cdot 10^6 = 1,25 \cdot 10^7$

Oppgave 2

$2^{2+ \frac x2} = 16 \\2^{2+ \frac x2} = 2^4 \\2 + \frac x2 = 4 \\ 4+x=8 \\ x=4$

Oppgave 3

$lg(2x-3)=0 \\ 10^{lg(2x-3)} = 10^0 \\ 2x-3 =1 \\ x=2$

Oppgave 5

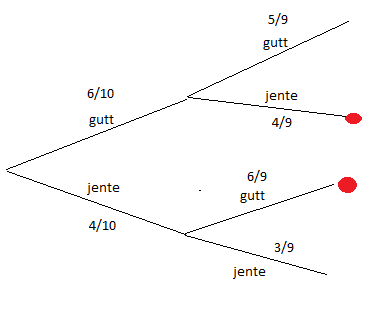
Det er to muligheter, gutt - jente og jente - gutt:

$P(en \quad av \quad hver) = \frac{6}{10} \cdot \frac{4}{9} + \frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15} $

Oppgave 6

a)

$x \ [0] \cup [3, \rightarrow>$

f er lik null for x lik 0 og 3. For x verdier større enn tre er f positiv.

Den deriverte til f er negativ fra x = 0 til x = 2. f avtar i dette området.

b)

Gjennomsnittlig vekstfart:

$\frac{\Delta x}{\Delta y} = \frac{-8 -0}{2} = -4$

Oppgave 7

$\frac {3x}{x+3} - \frac {3}{x-3} - \frac {x^2-12x+9}{x^2-9} = \\ \frac{3x(x-3)}{x+3} - \frac {3(x+3)}{(x-3)(x+3)} - \frac {x^2-12x+9}{(x+3)(x-3)} =\\ \frac {3x^2-9x-3x-9-x^2+12x-9}{(x+3)(x-3)}$