Lineær optimering: Forskjell mellom sideversjoner
Fra Matematikk.net
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| Linje 13: | Linje 13: | ||
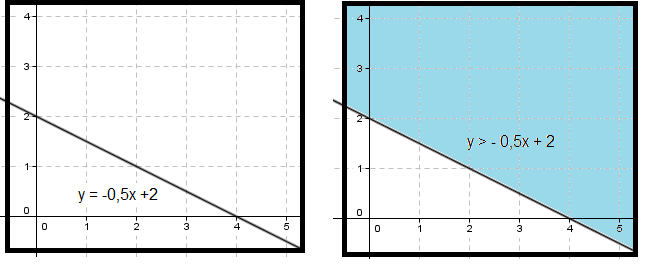
Over ser man linjen y = - 0,5x + 2. Alle verdier større enn -0,5x + 2 er markert med blått, y > -0,5x+2. | Over ser man linjen y = - 0,5x + 2. Alle verdier større enn -0,5x + 2 er markert med blått, y > -0,5x+2. | ||
En bedrift lager og selger saftis og fløteis. Bedriften regner med at | En bedrift lager og selger saftis og fløteis. Bedriften regner med at overskuddet blir 2 kroner per saftis og 3 kroner per fløteis. Vi setter | ||
x = antall saftis | x = antall saftis | ||
| Linje 19: | Linje 19: | ||
y = antall fløteis | y = antall fløteis | ||
Overskuddet blir da: | |||
Z = 2x + 3y | Z = 2x + 3y | ||
Sideversjonen fra 14. jun. 2013 kl. 06:17
Dette er en metode som kan brukes til å maksimere fortjenesten, ved å utnytte resursene eller innsatsfaktorene på en mest fornuftig måte. Resurser kan være
- Tid
- Arbeidskraft
- Kapital
- Råvarer
Man må være fortrolig med ulikheter.
Over ser man linjen y = - 0,5x + 2. Alle verdier større enn -0,5x + 2 er markert med blått, y > -0,5x+2.
En bedrift lager og selger saftis og fløteis. Bedriften regner med at overskuddet blir 2 kroner per saftis og 3 kroner per fløteis. Vi setter
x = antall saftis
y = antall fløteis
Overskuddet blir da:
Z = 2x + 3y