2P 2012 vår LØSNING: Forskjell mellom sideversjoner

Sideversjonen fra 16. mai 2015 kl. 15:16

Oppgave 1

a)

1,1,1,2,2,2,2,3,3,3,4,4,4,4,4,4,5,5,6,6

Variasjonsbredde : 6-1 = 5

Typetall : 4

Median: <math>\frac{3+4}{2}=3,5</math>

Gjennomsnitt: <math> \frac{3 \cdot1+4 \cdot2 + 3 \cdot 3 + 6 \cdot 4 + 2 \cdot 5 + 2 \cdot 6}{20} = \frac{66}{20} = 3,3</math>

b)

c)

d)

e)

f)

g)

Oppgave 2

Det største siffer vi observerer i høyre kolonne er 3, i tallet 131. Vi vet da at dette er et tall i 4 eller 5 tallssystemet. Prøver først femtallsystemet og finner at <math> 131_5=41_{10}</math>. Vi sjekker 120. Det kan være et tall i tre eller firetallsystemet. Vi tester i firetallsystemet <math> 120_4=24_{10}</math>. Videre har vi at <math> 100_2=4_{10}</math> og <math> 1011_3=31_{10}</math>. Utregningen er vist i tabellen nedenfor.

Grunntall fem	<math>5^2</math>	<math>5^1</math>	<math>5^0</math>
Utregnet	25	5	1
Mulig tall i femtallsystem	1	3	1
	<math>1 \cdot 25</math>	<math>+3 \cdot 5 </math>	<math>+1 \cdot1</math>	=41

Grunntall fire	<math>4^2</math>	<math>4^1</math>	<math>4^0</math>
Utregnet	16	4	1
Mulig tall i firetallsystem	1	2	0
	<math>1 \cdot 16</math>	<math>+2 \cdot 4 </math>	<math>+ 0 \cdot 1</math>	= 24

Oppgave 3

En noe uklar oppgave, men går ut fra at 30 gram potetskiver gir 150kcal.

a)

Spiser man en pose med 150 gram potetskiver får man i seg 150kcal ganger fem, fordi 30 går 5 ganger i 150. Det blir <math>150kcal \cdot 5 = 750kcal </math>

b)

Man får i seg ca. 17,5 gram karbohydrater

Del to

Oppgave 4

a)

De kan låne 920 tusen kroner.

b)

Etter ett år: <math>1150000kr \cdot 1,07 = 1230500kr = 1,23 mil.</math>

Etter ti år: <math>1150000kr \cdot 1,07^{10} = 2262224 = 2,26 mil </math>

Oppgave 5

a)

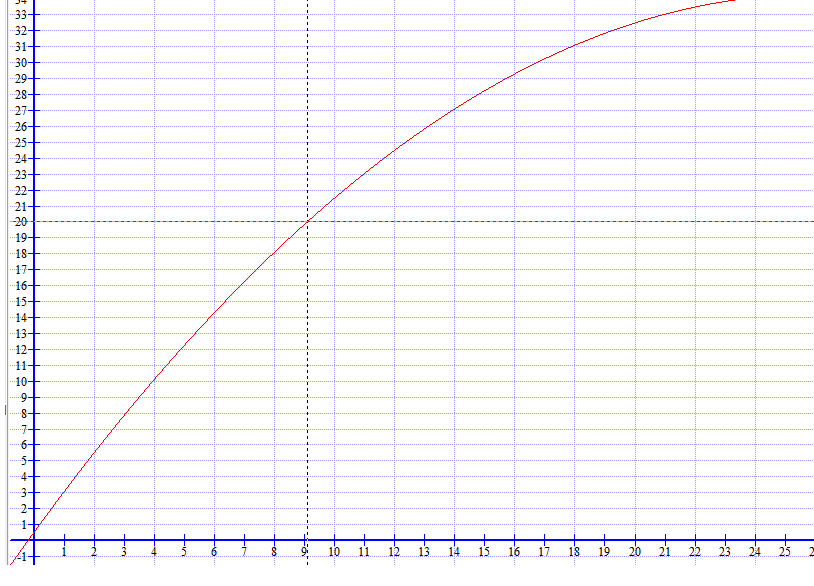
Når x er null er funksjonen 0,50, devs. at grisungen veier 0,5 kg ved fødselen.

b)

Da er alderen ca 9 måneder, lest fra grafen.

Gjennomsnittsøkning per måned blir <math> \frac{20kg - 0,5 kg}{9 mnd} =2,17 kg/mnd </math>

Oppgave 6

a)

To rosa: <math> \frac 2{10} \cdot \frac 19 = \frac 1{45}</math>

b)

En rosa og en i en annen farge: Det er to måter å gjøre dette på Rosa + annen farge eller annen farge + Rosa. Vi legger sammen de to sannsynlighetene:

c) To rosa er i samme farge og det finnes fire andre muligheter. Man ganger sannsynligheten i a med fem og får:

Oppgave 7

a)

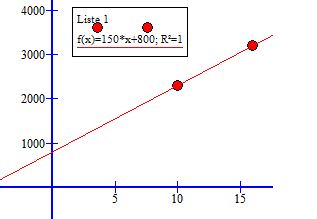
Dersom du liker algebra kan du løse oppgaven ved hjelp av to likninger med to ukjente. Siden vi har alle hjelpemiddler er det lettere å bruke lineær regresjon:

a = 150 kr

b = 800 kr

b)

Det koster 150 kr per tonn sand. Det koster 800 kr å få lastebilen til å kjøre til hytta, uansett hvor mye sand den frakter.

Oppgave 8

a)

Til denne oppgaven bruker vi statistikk kalkulatoren som du finner på dette nettstedet under ressurser. Den kan lastes ned til din skole-pc.

b)

c)

Verdi nr. fem bidro til å heve gjennomsnittet og til å øke spredningen. Når den utelates blir gjennomsnittet lavere og standardavviket mindre.

Oppgave 9

a)

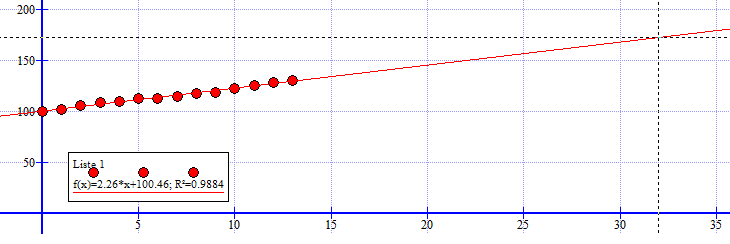
Rett linje: f(x) = 2,26x + 100,46

b)

KPI lest fra grafen i a: 172,8

c)

Dersom den øker med 2,5% fra 2001 til 2030:

Da ville KPI være 222,4 i 2030

Oppgave 10

a) Bruker pytagoras for å finne høyden i trekanten.

<math> \text{Høyde} = \sqrt{17^2 - 5^2} cm = 16,2cm </math>

Arealet er de fire trekantene pluss kvadratet i bunnen: <math> A = 4 \cdot \frac{G \cdot h}{2} + (10 cm)^2 =\frac{4 \cdot 10cm \cdot 16,2cm}{2} +100cm^2 = 425cm^2 </math>

b)

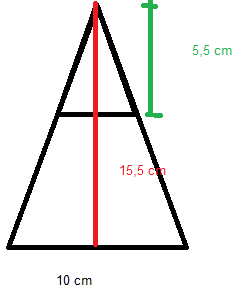
Bruker Pytagoras igjen... Høyden i en hvilken som helst av de rettvinklede trekantene utgjør hypotenusen i en rettvinklet trekant der det ene katetet er halve lengden av siden i bunnkvadratet. Det andre katetet er høyden i pyramiden. <math> \text{Pyramidehøyde} = \sqrt{(16,2 cm)^2 - (5 cm)^2} = 15,5 cm</math>

c)

Bruker formlikhet og ser at <math> \frac {x}{10} = \frac{5,5}{15,5} \\ x = 3,5 </math>

Hullet må være et kvadrat der sidene er ca. 3,5 cm.

@@ Linje 18: / Linje 18: @@
 c)
-Alternativ tre er riktig. Vekstfaktoren er 1-0,15 = 0,85.
 d)
-Den første trekanten er likesidet, alle vinkler er 60 grader og alle sider lik 3, hvilket gir en omkretts på 9.
-Den andre trekanten er rettvinklet. Da kan vi bruke Pytagoras for å finne lengden av det lengste katetet: <math>\sqrt{4^2-2^2} = \sqrt{12}</math>.
-Nå har man ikke kalkulator, da må man vite at kvadratroten av ni er tre og at kvadratroten av seksten er fire. Kvadratroent av tolv er derfor et sted mellom tre og fire. Dersom vi legger sammen 4 og 2 og kvadratroten av tolv ser man at det blir mer enn ni, altså har den rettvinklede trekanten størst omkrets.
 e)
-Varen følger indeksen:
-<math>\text{Kroneverdi} = \frac{100}{\text{konsumprisindeks}}  \\\text{Konsumprisindeks} = \frac{100}{\text{Kroneverdi}} = \frac{100}{0,8} = 125  </math>
-Dvs. varen koster kr. 125.
 f)
-Areal av sort flate er areal av sirkel minus areal av trekant:
-<math>  A = \pi r^2 - \frac{Gh}{2} = 3 \cdot 4^2 - \frac{8 \cdot 4}{2} = 48 - 16 = 32 </math>
 g)
-)
-[[file:venn_2p.png]]
-)
-Sannsynligheten for at en elev spiller håndball når vi vet at den spiller fotball blir seks av femten eller <math> \frac{6}{15} = \frac{2}{5}</math>
 ==Oppgave 2 ==