Funksjon: Forskjell mellom sideversjoner

Sideversjonen fra 5. feb. 2013 kl. 20:57

En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde <math>D_f</tex> . Et tall i definisjonsmengden <math>D_f</tex> svarer til et og bare et tall i verdimengden <math>V_f</tex>. Et tall i verdimengden kan på den annen side svare til flere verdier i definisjonsmengden. Selve "broen" er funksjonsuttrykket. Funksjonsutrykket sier noe om hvordan tallene i definisjonsmengden skal behandles.

Sideversjonen fra 15. aug. 2011 kl. 04:58 vis kilde Administrator (diskusjon \| bidrag) Byråkrater, Administratorer 23 182 redigeringer Ingen redigeringsforklaring ← Forrige endring		Sideversjonen fra 5. feb. 2013 kl. 20:57 vis kilde Vaktmester (diskusjon \| bidrag) Byråkrater, Grensesnittadministratorer, Administratorer 3 541 redigeringer m Teksterstatting – «<tex>» til «<math>» Neste endring →
Linje 1:		Linje 1:
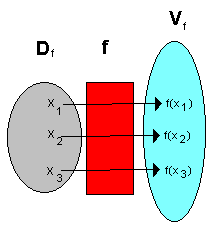
	En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde <~~tex~~>D_f</tex> . Et tall i definisjonsmengden <~~tex~~>D_f</tex> svarer til et og bare et tall i verdimengden <~~tex~~>V_f</tex>. Et tall i verdimengden kan på den annen side svare til flere verdier i definisjonsmengden. Selve "broen" er funksjonsuttrykket. Funksjonsutrykket sier noe om hvordan tallene i definisjonsmengden skal behandles.		En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde <math>D_f</tex> . Et tall i definisjonsmengden <math>D_f</tex> svarer til et og bare et tall i verdimengden <math>V_f</tex>. Et tall i verdimengden kan på den annen side svare til flere verdier i definisjonsmengden. Selve "broen" er funksjonsuttrykket. Funksjonsutrykket sier noe om hvordan tallene i definisjonsmengden skal behandles.

	[[Bilde:Funksjon.gif]]		[[Bilde:Funksjon.gif]]