Platonske legemer: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Vi har fem platonske legemer. De kalles platonske fordi de først nevnes av Platon. De er regelmessige polyedre der sideflatene er regulære polygoner (mangekanter). • n er antall po... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
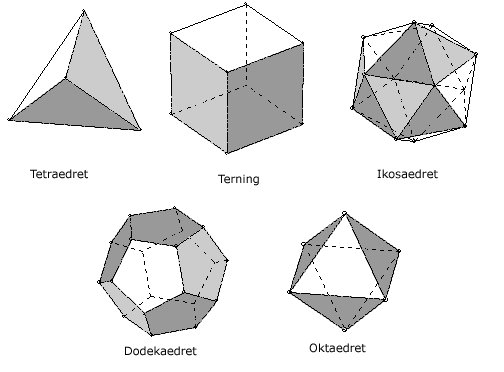
Vi har fem platonske legemer. De kalles platonske fordi de først nevnes av Platon. De er regelmessige polyedre der sideflatene er regulære polygoner (mangekanter). | Vi har fem platonske legemer. De kalles platonske fordi de først nevnes av Platon. De er regelmessige polyedre der sideflatene er regulære polygoner (mangekanter). | ||
[[Bilde:Platonske.gif]] <p></p> | |||
• n er antall polygoner som møtes i et hjørne | • n er antall polygoner som møtes i et hjørne <p></p> | ||
• m er antall hjørner i hvert polygon | • m er antall hjørner i hvert polygon <p></p> | ||
• f er antall flater i polyedrene | • f er antall flater i polyedrene <p></p> | ||
• e er antall kantlinjer i polyedrene | • e er antall kantlinjer i polyedrene<p></p> | ||
• v er antall hjørner i polyedrene | • v er antall hjørner i polyedrene <p></p> | ||
Vi har følgende sammenheng: | Vi har følgende sammenheng:<p></p> | ||
Sideversjonen fra 31. jul. 2011 kl. 09:36
Vi har fem platonske legemer. De kalles platonske fordi de først nevnes av Platon. De er regelmessige polyedre der sideflatene er regulære polygoner (mangekanter).
• n er antall polygoner som møtes i et hjørne
• m er antall hjørner i hvert polygon
• f er antall flater i polyedrene
• e er antall kantlinjer i polyedrene
• v er antall hjørner i polyedrene
Vi har følgende sammenheng:
m
n
f
e
v
Tetraedret
3
3
4
6
4
Oktaedret
3
4
8
12
6
Ikosaedret
3
5
20
30
12
Terningen
4
3
6
12
8
Dodekaedret
5
3
12
30
20
Ved å følge linken nedenfor finner dere interaktive legemer som kan beveges.