Monoton: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Dersom en funksjon f(x) er avtagende har vi følgende: f(x1) ≥ f(x2), der x1 < x2. Dersom en funksjon f(x) er voksende har vi følgende: f(x1) ≤ f(x2), der x1 < x2. Dersom en ... |
Ingen redigeringsforklaring |
||
| Linje 7: | Linje 7: | ||
f(x1) ≤ f(x2), der x1 < x2. | f(x1) ≤ f(x2), der x1 < x2. | ||
[[Bilde:Monotoni.gif]] | |||
Dersom en funksjon f(x) er strengt voksende har vi følgende: | Dersom en funksjon f(x) er strengt voksende har vi følgende: | ||
f(x1) < f(x2), der x1 < x2. | |||
Dersom en funksjon f(x) er strengt avtagende har vi følgende: | Dersom en funksjon f(x) er strengt avtagende har vi følgende: | ||
Siste sideversjon per 19. jul. 2011 kl. 05:43
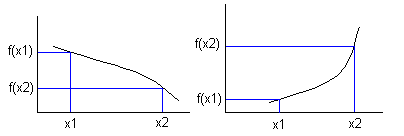
Dersom en funksjon f(x) er avtagende har vi følgende:
f(x1) ≥ f(x2), der x1 < x2.
Dersom en funksjon f(x) er voksende har vi følgende:
f(x1) ≤ f(x2), der x1 < x2.
Dersom en funksjon f(x) er strengt voksende har vi følgende:
f(x1) < f(x2), der x1 < x2.
Dersom en funksjon f(x) er strengt avtagende har vi følgende:
f(x1) > f(x2), der x1 < x2.
Av dette følger også at en funksjon er monoton dersom den førstederiverte av funksjonen ikke forandrer fortegn.