Konveks funksjon: Forskjell mellom sideversjoner
Fra Matematikk.net
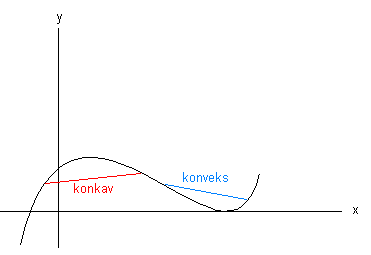
Ny side: En reell funksjon av en eller flere variable sies å være konveks dersom en korde som forbinder to vilkårlige punkter på grafen ligger over eller på grafen. En funksjon sies å være s... |
Ingen redigeringsforklaring |
||
| Linje 2: | Linje 2: | ||
En funksjon sies å være strengt konveks dersom alle tilfeldige korder mellom to punkter på grafen ligger over grafen. | En funksjon sies å være strengt konveks dersom alle tilfeldige korder mellom to punkter på grafen ligger over grafen. | ||
[[Bilde:Konkav.gif]] | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||