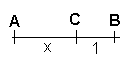Gylne snitt: Forskjell mellom sideversjoner

Sideversjonen fra 14. jul. 2011 kl. 05:07

Det gylne snitt kalles også for høydeling og er et forhold mellom oppdelingen av linjestykker.

Et linjestykke er høydelt dersom forholdet mellom største og minste del er lik forholdet mellom hele linjestykket og den største delen.

Dersom linjen over er høydelt må

Fra det følger :

Når vi løser likningen og forkaster den negative løsningen får vi

<tex>x = \frac{1+ \sqrt5}{2} \approx 1,618</tex>

Vi kaller det gylne snitt for den greske bokstaven fi, Φ, og får:

<tex> \phi = \frac{1+ \sqrt5}{2} \approx 1,618</tex>

Man har videre

<tex> \phi^2 = \phi + 1 \\ \frac{1}{\phi}= \phi - 1 \approx 0,618</tex>

Forholdet brukes mye i kunst og arkitektur.

@@ Linje 21: / Linje 21: @@
 <tex> \phi = \frac{1+ \sqrt5}{2} \approx 1,618</tex>
-Fra andregradslikningen Φ2 = Φ + 1
+Man har videre<p></p>
+<tex> \phi^2 = \phi + 1 \\ \frac{1}{\phi}= \phi - 1 \approx 0,618</tex>
-ser vi at 1/Φ = Φ - 1 ≈ 0,618
-Dersom vi har et linjestykke med lengde en vil høydelingen være et punkt 0,618 fra den ene enden og 0,382 fra den andre enden.
-Eks:
-En stokk har lengde 128 cm. Høydel stokken.
-Vi har flere muligheter for løsning og det finnes to punkter på stokken som tilfredstiller kravet i oppgaven. Figuren nedenfor viser mulighetene. vi kan dele stokken opp i to lengder; 1 og 1,618, til sammen 2,618 eller, kanskje mer naturlig
-i 0,382 og 0,618 til sammen 1.
-Begge tankerekker gir samme resultat:
-cm · 0,382 = 48,5cm eller
-cm · 0,618 = 78,5cm
-gir begge delingspunktene regnet fra en side. En av utregningene vil gi begge punktene om du bruker den samme utregningen fra begge ender av staven.
-Figuren illustrerer også tankemåten:
-(1,618 / 2,618) = 0,618 og (1,0 / 2,618) = 0,382 hvilket gir samme resultat som over.
 Forholdet brukes mye i kunst og arkitektur.