Eksponentialfunksjonen

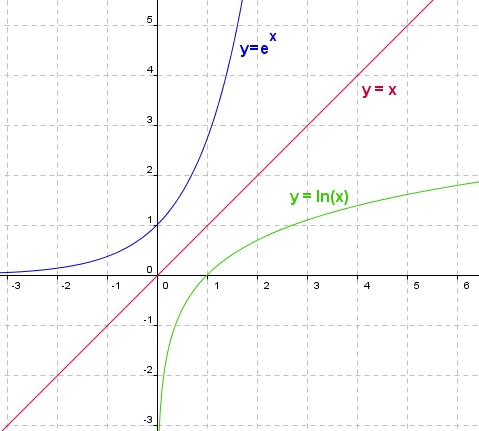
Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler hverandre om linjen y = x.

Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende:

• <tex> e^p \cdot e^q = e^{(p+q)} </tex>

• <tex> \frac{e^p}{e^q} = e^{(p-q)} </tex>

• <tex> (e^p)^q = e^{(p\cdot q)} </tex>

Nedenfor er det plottet noen forskjellige funksjonen der eksponentialfunksjonen inngår.

---