Praktisk romgeometri: Forskjell mellom sideversjoner
Fra Matematikk.net
| Linje 16: | Linje 16: | ||
z = z_0 + ct \right]</tex> | z = z_0 + ct \right]</tex> | ||
I plantet er det slik at to linjer som ikke er parallelle vil skjære hverandre. I rommet er det nødvendigvis ikke tilfelle. To linjer som ikke er parallelle og som ikke skjærer hverandre sies å være vindskeive. | |||
=== Avstand mellom punkt og linje === | === Avstand mellom punkt og linje === | ||
Sideversjonen fra 2. jan. 2011 kl. 08:17
Nedenfor finner man en oversikt over de vanligste spørsmål som dukker opp i forbindelse med punkter, linjer og plan.
Punkt
Avstand mellom to punkter
Avstanden d mellom punktene A og B er gitt ved <tex>d=|\vec{AB}|= \sqrt{(x_B - x_A)^2 + (y_B -y_A)^2 + (z_B - z_A)^2} </tex>
Altså lik lengden av AB vektor.
Linje
En rett linje m som går gjennom punktet <tex>p = (x_0 , y_0 , z_0) </tex> og har rettningsvektor <tex> \vec{n} = (a, b, c) </tex> har parameterfremstillingen: <tex> m: \left [ x = x_0 + at\\ y = y_0 + bt \\ z = z_0 + ct \right]</tex>
I plantet er det slik at to linjer som ikke er parallelle vil skjære hverandre. I rommet er det nødvendigvis ikke tilfelle. To linjer som ikke er parallelle og som ikke skjærer hverandre sies å være vindskeive.
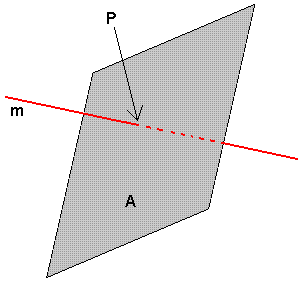
Avstand mellom punkt og linje
Avstand mellom to linjer
Vinkel mellom to linjer
Ligger punktet på linja?
Plan
Vinkel mellom linje og plan
Avstand linje og plan
Avstand mellom punkt og plan
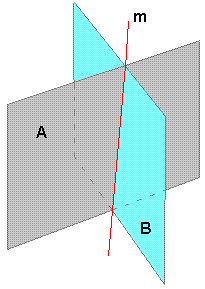
Skjæring mellom to plan