1T 2017 vår LØSNING

Denne oppgaven som PDF

diskusjon av denne oppgaven

Løsning laget av mattepratbruker Lektor Nilsen

Løsning bidratt av Lektor Ørjan Augedal, Fana privat gymnas

Løsning laget av mattepratbruker rekel

Løsning laget av mattepratbruker mattemarkus

Oppgave 1

$\frac{0,72 \cdot 10^8}{60 \cdot 10^{-8}} = \frac{72 \cdot 10^6}{6 \cdot 10^{-7}} = 12 \cdot 10^{6+7} = 1,2 \cdot 10^{14}$

Oppgave 2

$4^0 + 2^{-3} \cdot (2^3)^2 = 1+ 2^3 = 9$

Oppgave 3

$\sqrt{20} + \sqrt 5 - \frac{\sqrt{160}}{\sqrt 2}= 2 \sqrt 5 +\sqrt 5 - \frac{\sqrt4 \cdot \sqrt4 \cdot \sqrt 2 \cdot \sqrt 5}{\sqrt 2} \\ 2 \sqrt 5 + \sqrt5 - 4 \sqrt 5 = - \sqrt 5$

Oppgave 10

a)

$f(x)>0 \Rightarrow x \in <4, \rightarrow>$

b)

$f´(x) >0 \Rightarrow x \in < \leftarrow,1> \cup <3, \rightarrow>$

Oppgave 11

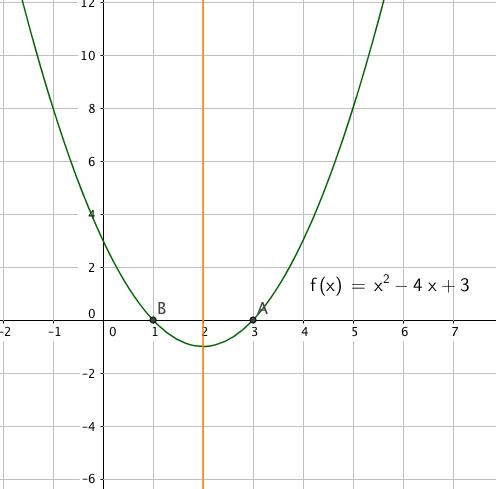
a)

Nullpunkter:

$ f(x)=0 \\ x^2-4x+3=0 \\ x= \frac{4 \pm \sqrt{16 - 4 \cdot 3}}{2} \\ x = 1 \vee x= 3$

Nullpunkter (1,0) og (3,0).

b)

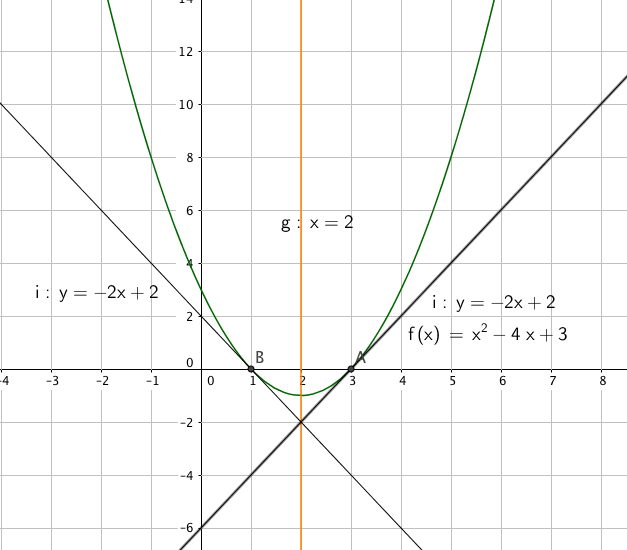
c)

V finner den x verdi som gir f´(x) = 2. $f´(x) =2 \\ 2x-4 =2 \\ x=3$

Vi vet at f(3) = 0

Likningen for tangenten blir da: $y = ax + b \\ 0 = 2 \cdot 3 + b \\ b = -6$

y= 2x - 6 er likningen for tangenten med stigningstall 2.