1T 2016 vår LØSNING: Forskjell mellom sideversjoner
| Linje 36: | Linje 36: | ||
==Oppgave 10== | ==Oppgave 10== | ||
Vi observerer at graf A er den eneste som har et minimum for en negativ x verdi. 2x + 6 = 0 gir løsning for x = - 3, altså er | |||
h(x) funksjonen til graf A. | |||
Graf B har ingen nullpunkter : $b^2 - 4ac < 0$ | |||
==Oppgave 11== | ==Oppgave 11== | ||
Sideversjonen fra 29. mai 2016 kl. 11:38
Mer diskusjon av denne oppgaven
Løsning av denne oppgaven laget av mattepratbruker LektorH
DEL EN
Oppgave 1
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
a)
b)
Oppgave 6
Oppgave 7
Oppgave 8
Oppgave 9
a)
b)
c)
Oppgave 10
Vi observerer at graf A er den eneste som har et minimum for en negativ x verdi. 2x + 6 = 0 gir løsning for x = - 3, altså er
h(x) funksjonen til graf A.
Graf B har ingen nullpunkter : $b^2 - 4ac < 0$
Oppgave 11
a)
b)
Oppgave 12
a)
b)
Oppgave 13
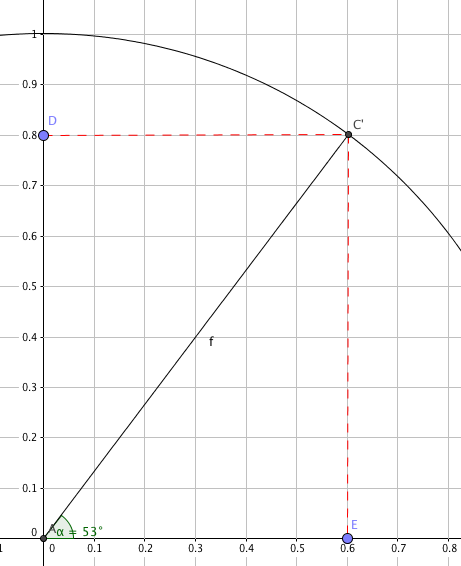
Vi leser av figuren:
$cos 53^{\circ} \approx 0,6 \\ sin 53^{\circ} \approx 0,8$
Tangens:
$tan 53^{\circ} \approx \frac 86 \approx 1,33 $
Oppgave 14
a)
Funksjonen har ekstremalpunkter når den deriverte er null. For x = 0 og x = 4 er det tillfelle. x = 0 er et toppunkt fordi den deriverte skifter fra positiv til negativ verdi, og x = 4 er et bunnpunkt fordi den deriverte skifter fra negativ til positiv verdi.
b)
Likningen for en rett linje er y = ax + b
I punktet (2,-3) er den deriverte lik -2. Det gir y= -2x + b
Setter så punktet (2, -3) inn for x og y for å finne b: $ -3 = -2 \cdot 2 +b$ som gir b=1.
Likningen blir da:
y = -2x + 1