Løsning del 2 utrinn Vår 15 eksempeloppgave: Forskjell mellom sideversjoner
| Linje 123: | Linje 123: | ||
[[File:mat0010-e-15-7abc.png]] | [[File:mat0010-e-15-7abc.png]] | ||
===a)=== | |||
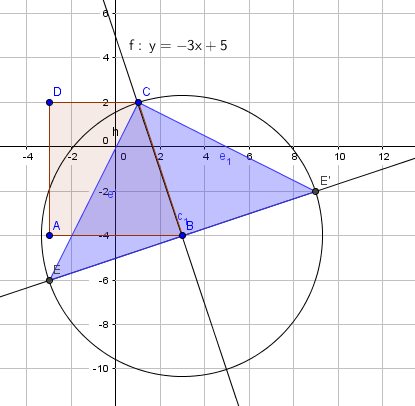
Det er et trapes. | |||
===b)=== | |||
Se figur over. | |||
===c)=== | |||
Ser fra figuren over at punktene () og () tilfredstiller kravene til E. | |||
==Oppgave 8== | ==Oppgave 8== | ||
Sideversjonen fra 15. des. 2015 kl. 12:25
- Oppgaven Del 1 som pdf
- Løsning del 1
- Oppgaven Del 2 som pdf
- Løsning på oppgaven som pdf
- Løsning på oppgaven på doc-format
- Løsning på oppgave 4, 7, 9 og 10 løst med ggb cas og grafikk som pdf
- Løsning av alle oppgaver som videoer
Oppgave 1
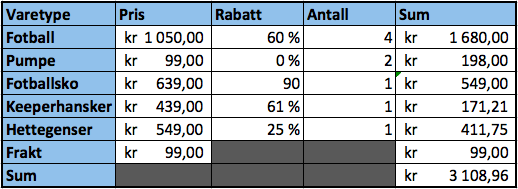
a)
Hun må betale kr. 3108,96.
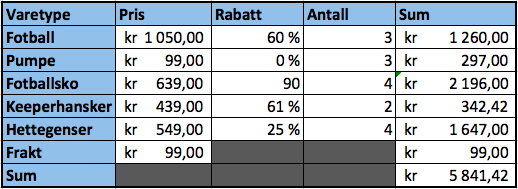
b)
Se figur i a. Hun må betale 5841,42 kroner.
Oppgave 2
a)
b)
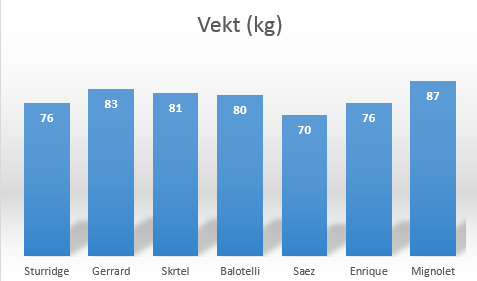
Et linjediagram indikerer kontinuitet over tid, mellom måleunkter. Det er ingen sammenheng mellom spillernes masse (vekt) over tid, eller på andre måter.
Oppgave 3
a)
$4 \cdot 4 \cdot 3 = 48$ kombinasjoner.
b)
Vi forutsetter at skjorte 1 og 2 er identisk med skjorte 2 og 1.
Om du trekker skjorte 1 kan du i tillegg trekke 2, 3 eller 4, altså 3 muligheter (1,2),(1,3),(1,4).
Om du trekker skjorte 2 kan du i tillegg trekke 3 eller 4, altså to muligheter (2,3), (2,4)
Om du trekker skjorte 3 kan du også trekke 4, altså en mulighet (3,4)
Det blir tilsammen seks kombinasjoner.
Litt mere matematisk kan det skrives slik:
$4C2 = \frac{4!}{(2!(4-2)!} = 3\cdot 2 \cdot 1 = 6$
Oppgave 4
a)
$V(r)= \frac 43 \pi r^3 $
$r = \frac{O}{2\pi} = 10,66 cm$
$V(10,66 cm) = \frac43 \cdot \pi \cdot (10,66 cm)^3 \\ V(10,66cm) = 5079 cm^3$
5000 kubikksentimeter tilsvarer 5 liter.
b)
Overflate av kule: $ O(r) = 4 \pi r^2 \\ O(10,66 cm)= 4 \cdot \pi \cdot (10,66 cm)^2 \\O(10,66 cm) = 1428 cm^2 $
c)
$r=\sqrt{ \frac {O}{4 \pi}} = \sqrt{\frac{1000cm^2}{4 \pi}} \approx 8,92 cm $
Volum:
$V(8,92)= \frac 43 \pi (8,92 cm)^3 = 2973,5 cm^3$
Volumet ligger på ca. 3 liter, så da er vel dette en 3er fotball.
Oppgave 5
a)
En drikk som er blandet i forholdet 1:2 består av 3 deler. Det er $\frac 13 \cdot 2 liter = \frac 23$ liter næringsstoff og $\frac 43$ liter vann, i en blanding på 2 liter..
b)
Dersom 2 deler vann er $\frac 43$ er en del vann $\frac 23$. Dvs det må tilsettes to tredje dels liter for at forholdet skal bli 1:3.
Oppgave 6
a)
Trekant ABC er en 30, 60, 90 graders trekant. Da er hypotenusen dobbelt så lang som korteste katet, altså 16 meter.
b)
$AB = \sqrt{(16m)^2-(8m)^2} \approx 13,85 m$
c)
$AD = \sqrt{(13,85m)^2+(15,32m)^2} = 20,65m$
$AE = \sqrt{(20,65m)^2+(2,44m)^2} = 20,79m$
Gjennomsnittsfart fra A til E
$v = \frac st = \frac{20,79m}{0,8m} = 26 m/s$
Oppgave 7
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Det er et trapes.
b)
Se figur over.
c)
Ser fra figuren over at punktene () og () tilfredstiller kravene til E.
Oppgave 8
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.
Oppgave 9
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
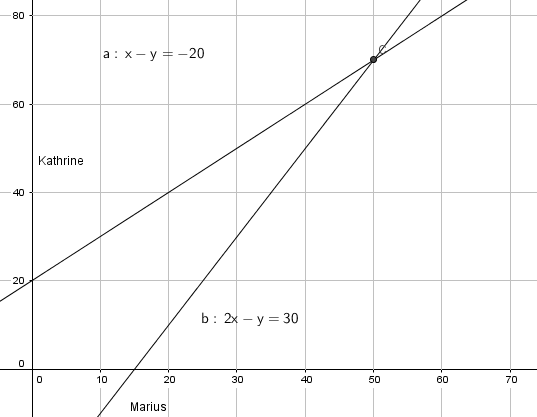
Marius: "Gi meg 10 klinkekuler, så har vi like mange" gir oss: x +10 = y - 10 som er lik x - y = -20.
Kathrine: "Hvis du i stedet gir meg 10 klinkekuler, så vil jeg ha dobblt så mange som deg" gir oss:
$2(x - 10) = y+ 10 \\ x - 20 = y + 10 \\ 2x -y = 30$
b)
Vi ser at Marius har 50 kuler og Kathrine har 70.
c)
\begin{bmatrix} x-y = -20 \\ 2x-y=30 \end{bmatrix} \begin{bmatrix} -x+y=20 \\ 2x-y = 30 \end{bmatrix} \begin{bmatrix} 2x-x=20+30 \end{bmatrix}
\begin{bmatrix} x = 50 \end{bmatrix}
Innsatt for x = 50 gir det 50 - y = -20, dvs y = 70
$x=50 \wedge y=70$
Marius har 50 kuler og Kathrine har 70.
Oppgave 10
Løsning på denne oppgaven som video laget av Mette Bendiksen
a)
Område 1: $20m \cdot 50m = 1000m^2$
Område 2: $60m \cdot 10m = 600m^2$
b)
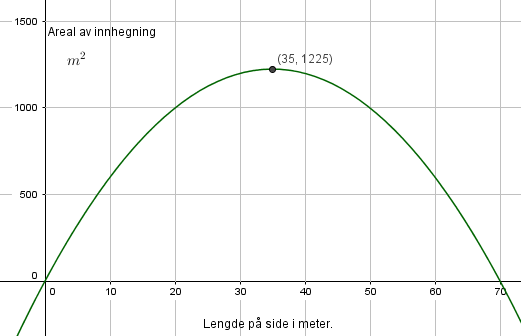
Dersom to av sidene er x er lengden som er igjen til de to andre sidene lik 140- 2x. Når man deler på 2 finner man at en av disse sidene må være 70-x.
$A(x)= x(70 - x) = -x^2 +70x$
x kan ligge mellom 0 og 70 meter. $x \in [0, 70]$